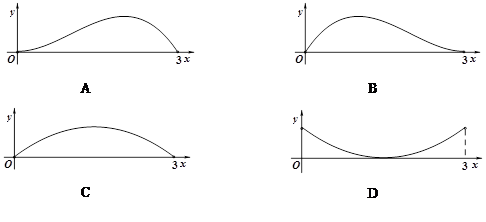已知x与y之间的几组数据如下表:
| x |
0 |
1 |
2 |
3 |
| y |
0 |
2 |
6 |
7 |
则y与x的线性回归方程 =
=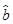 x+
x+ 必过点( )
必过点( )
A.(1,2) B.(2,6) C. 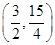 D.(3,7)
D.(3,7)
已知回归直线的斜率的估计值为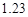 ,样本点的中心为
,样本点的中心为 ,则回归直线方程为
,则回归直线方程为
A.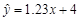 |
B.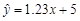 |
C.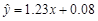 |
D. |
某工厂产生的废气经过过滤后排放,过滤过程中废气的污染物数量 与时间
与时间 间的关系为
间的关系为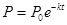 .若在前5个小时消除了
.若在前5个小时消除了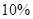 的污染物,则污染物减少
的污染物,则污染物减少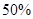 所需要的时间约为( )小时.(已知
所需要的时间约为( )小时.(已知 =0.3010,
=0.3010,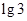 =0.4771)
=0.4771)
| A.26 | B.33 | C.36 | D.42 |
一名小学生的年龄和身高(单位:cm)的数据如下:
年龄 |
6 |
7 |
8 |
9 |
身高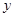 |
118 |
126 |
136 |
144 |
由散点图可知,身高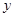 与年龄
与年龄 之间的线性回归直线方程为
之间的线性回归直线方程为 ,预测该学生10岁时的身高为( )
,预测该学生10岁时的身高为( )
A.154 B. 153 C.152 D. 151
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
| 日期 |
12月1日 |
12月2日 |
12月3日 |
12月4日 |
12月5日 |
| 温差x/℃ |
10 |
11 |
13 |
12 |
8 |
| 发芽数y /颗 |
23 |
25 |
30 |
26 |
16 |
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程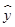 =bx+a;
=bx+a;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为
A.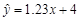 |
B.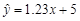 |
C. |
D. |
观察下面频率等高条形图,其中两个分类变量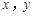 之间关系最强的是( )
之间关系最强的是( )
A. B. C. D.
某单位为了了解用电量y度与气温x℃之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
| x |
18 |
13 |
10 |
-1 |
| y |
25 |
34 |
39 |
62 |
由表中数据得线性回归方程y=-2x+a,预测当气温为-4 ℃时,用电量的度数约为 .
某市政府调查市民收入增减与旅游愿望的关系时,采用独立性检验法抽查了3 000人,计算发现K2=6.023,则根据这一数据查阅下表,市政府断言市民收入增减与旅游愿望有关系的可信程度是_______。
| P(K2≥k) |
0.25 |
0.15 |
0.10 |
0.025 |
0.010 |
0.005 |
| k |
1.323 |
2.072 |
2.706 |
5.024 |
6.635 |
7.879 |
某商场在今年端午节的促销活动中,对6月2日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则11时至12时的销售额为( )
| A.8万元 | B.10万元 |
| C.12万元 | D.15万元 |
某教育机构随机某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成[0,5),[5,10),[10,15),[15,20),[20,25),[25,30),[30,35),[35,40]时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )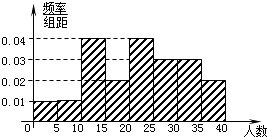

已知边长为3的正方形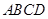 与正方形
与正方形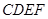 所在的平面互相垂直,
所在的平面互相垂直,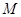 为线段
为线段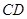 上的动点(不含端点),过
上的动点(不含端点),过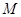 作
作 交
交 于
于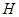 ,作
,作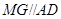 交
交 于
于 ,连结
,连结 .设
.设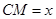
 ,则下面四个图象中大致描绘了三棱锥
,则下面四个图象中大致描绘了三棱锥 的体积
的体积 与变量
与变量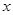 变化关系的是
变化关系的是