苏教版选修2-3高二数学双基达标3.2练习卷
由一组样本数据(x1,y1),(x2,y2),…,(xn,yn)得到线性回归方程 =
= x+
x+ ,那么下列说法正确的是________.
,那么下列说法正确的是________.
①直线 =
= x+
x+ 必经过点(
必经过点( ,
, );
);
②直线 =
= x+
x+ 至少经过点(x1,y1),(x2,y2),…,(xn,yn)中的一个点;
至少经过点(x1,y1),(x2,y2),…,(xn,yn)中的一个点;
③直线 =
= x+
x+ 的斜率为
的斜率为 ;
;
④直线 =
= x+
x+ 和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差
和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差 是该坐标平面上的直线与这些点的最小偏差.
是该坐标平面上的直线与这些点的最小偏差.
某小卖部为了了解冰糕销售量y(箱)与气温x(℃)之间的关系,随机统计了某4天卖出的冰糕的箱数与当天气温,并制作了对照表(如下表所示),且由表中数据算得线性回归方程 =
= x+
x+ 中的
中的 =2,则预测当气温为25 ℃时,冰糕销量为________箱.
=2,则预测当气温为25 ℃时,冰糕销量为________箱.
| 气温/℃ |
18 |
13 |
10 |
-1 |
| 冰糕/箱 |
64 |
38 |
34 |
24 |
已知对一组观测值(xi,yi)(i=1,2,…,n)作出散点图后,确定具有线性相关关系,若对于 =
= +
+ x,求得
x,求得 =0.51,
=0.51, =61.75,
=61.75, =38.14,则线性回归方程为________.
=38.14,则线性回归方程为________.
在某种产品表面进行腐蚀性刻线实验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值,如下表:
| x/s |
5 |
10 |
15 |
20 |
30 |
40 |
50 |
60 |
70 |
90 |
120 |
| y/μm |
6 |
10 |
10 |
13 |
16 |
17 |
19 |
23 |
25 |
29 |
46 |
用散点图及相关系数两种方法判断x与y的相关性.
以下关于线性回归的判断,正确的是________.
①散点图中所有点都在一条直线附近,这条直线为回归直线
②散点图中的绝大多数点都在回归直线的附近,个别特殊点不影响线性回归性
③已知直线方程为 =0.50x-0.81,则x=25时,
=0.50x-0.81,则x=25时, 为11.69
为11.69
④回归直线方程的意义是它反映了样本整体的变化趋势
对有线性相关关系的两个变量建立的线性回归方程 =
= +
+ x,关于回归系数
x,关于回归系数 ,下面叙述正确的是________.
,下面叙述正确的是________.
①可以小于0;②大于0;③能等于0;④只能小于0.
对具有线性相关关系的变量x、y有观测数据(xi,yi)(i=1,2,…,10),它们之间的线性回归方程是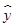 =3x+20,若
=3x+20,若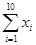 =18,则
=18,则 =________.
=________.
一唱片公司欲知唱片费用x(十万元)与唱片销售量Y(千张)之间的关系,从其所发行的唱片中随机抽选了10张,得如下的资料: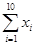 =28,
=28,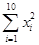 =303.4,
=303.4,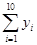 =75,
=75, =598.5,
=598.5,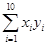 =237,则y与x的相关系数r的绝对值为________.
=237,则y与x的相关系数r的绝对值为________.
为了对新产品进行合理定价,对该产品进行了试销试验,以观察需求量Y(单位:千件)对于价格x(单位:千元)的反应,得数据如下:
| x/千元 |
50 |
70 |
80 |
40 |
30 |
90 |
95 |
97 |
| y/千件 |
100 |
80 |
60 |
120 |
135 |
55 |
50 |
48 |
(1)若y与x之间具有线性相关关系,求y对x的回归直线方程;
(2)若成本x=y+500,试求:
①在盈亏平衡条件下(利润为零)的价格;
②在利润为最大的条件下,定价为多少?
一个车间为了规定工时定额.需要确定加工零件所花费的时间,为此进行了10次试验.测得的数据如下:
| 零件数x/个 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
| 加工时间y/分 |
62 |
68 |
75 |
81 |
89 |
95 |
102 |
108 |
115 |
122 |
(1)y与x是否具有线性相关关系?
(2)如果y与x具有线性相关关系,求回归直线方程;
(3)根据求出的回归直线方程,预测加工200个零件所用的时间为多少?
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
| 日期 |
12月1日 |
12月2日 |
12月3日 |
12月4日 |
12月5日 |
| 温差x/℃ |
10 |
11 |
13 |
12 |
8 |
| 发芽数y /颗 |
23 |
25 |
30 |
26 |
16 |
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程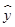 =bx+a;
=bx+a;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
 粤公网安备 44130202000953号
粤公网安备 44130202000953号