[湖北]2013-2014学年湖北荆门市高二上学期期末质量检测理数学试卷
给出命题:“若 ,则
,则 ”,在它的逆命题、否命题、逆否命题中,真命题的个数是
”,在它的逆命题、否命题、逆否命题中,真命题的个数是
| A.0个 | B.1个 | C.2个 | D.3个 |
已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为
A.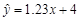 |
B.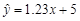 |
C. |
D. |
如图是用模拟方法估计圆周率π值的程序框图,P表示估计结果,则图中空白框内应填入
A.P= |
B.P= |
C.P= |
D.P= |
某运动会组委会要派五名志愿者从事翻译、导游、礼仪三项工作,要求每项工作至少有一人参加,则不同的派给方案共有
| A.150种 | B.180种 | C.240种 | D.360种 |
甲乙两组统计数据用茎叶图表示,设甲乙两组数据的平均数分别为
 ,中位数分别为
,中位数分别为 ,
, ,则
,则
A. < < , , > > |
B. < < , ,    |
C. > > , ,  > > |
D. > > , ,  < < |
已知双曲线 的一条渐近线方程是
的一条渐近线方程是 ,它的一个焦点在抛物线
,它的一个焦点在抛物线 的准线上,则双曲线的方程为
的准线上,则双曲线的方程为
A. |
B. |
C. |
D. |
△ 中,角
中,角 成等差数列是
成等差数列是 成立的
成立的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设 为整数
为整数 ,若
,若 和
和 被
被 除得的余数相同,则称
除得的余数相同,则称 和
和 对
对 同余记为
同余记为 ,已知
,已知 …
… ,
,  ,则
,则 的值可以是
的值可以是
| A.2013 | B.2012 | C.2011 | D.2010 |
如果随机变量X~N(-1,σ2),且P(-3≤X≤-1)=0.4,则P(X≥1)=________.
某中学高一年级有学生600人,高二年级有学生450人,高三年级有学生750人,每个学生被抽到的可能性均为0.2,若该校取一个容量为n的样本,则n= .
多选题是标准化考试的一种题型,一般是从A、B、C、D四个选项中选出所有正确的答案.在一次考试中有5道多选题,某同学一道都不会,他随机的猜测,则他答对题数的期望值为 .
欧阳修《卖油翁》中写到:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.已知铜钱是直径为4cm的圆面,中间有边长为1cm的正方形孔,若随机向铜钱上滴一滴油(油滴整体不出边界),则油滴整体(油滴是直径为0.2cm的球)正好落入孔中的概率是 (不作近似计算).
设 分别是双曲线
分别是双曲线 的左、右焦点,若双曲线右支上存在一点
的左、右焦点,若双曲线右支上存在一点 ,使
,使 (
( 为原点),且
为原点),且 ,则双曲线的离心率为 .
,则双曲线的离心率为 .
已知命题p: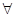 x∈[1,2],x2-a≥0,命题q:
x∈[1,2],x2-a≥0,命题q: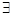 x0∈R,x+2ax0+2-a=0,若“p且q”为真命题,求实数a的取值范围.
x0∈R,x+2ax0+2-a=0,若“p且q”为真命题,求实数a的取值范围.
为考查某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:
| |
患病 |
未患病 |
总计 |
| 没服用药 |
20 |
30 |
50 |
| 服用药 |
 |
 |
50 |
| 总计 |
 |
 |
100 |
设从没服用药的动物中任取两只,未患病数为 ;从服用药物的动物中任取两只,未患病数为
;从服用药物的动物中任取两只,未患病数为 ,工作人员曾计算过
,工作人员曾计算过 .
.
(1)求出列联表中数据 的值;
的值;
(2)能够以99%的把握认为药物有效吗?参考公式: ,其中
,其中 ;
;
①当K2≥3.841时有95%的把握认为 、
、 有关联;
有关联;
②当K2≥6.635时有99%的把握认为 、
、 有关联.
有关联.
某市准备从7名报名者(其中男4人,女3人)中选3人到三个局任副局长.
(1)设所选3人中女副局长人数为X,求X的分布列和数学期望;
(2)若选派三个副局长依次到A、B、C三个局上任,求A局是男副局长的情况下,B局为女副局长的概率.
从某校高二年级 名男生中随机抽取
名男生中随机抽取 名学生测量其身高,据测量被测学生的身高全部在
名学生测量其身高,据测量被测学生的身高全部在 到
到 之间.将测量结果按如下方式分成
之间.将测量结果按如下方式分成 组:第一组
组:第一组 ,第二组
,第二组 , ,第八组
, ,第八组 ,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
频率分布表如下:
| 分组 |
频数 |
频率 |
频率/组距 |
| |
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
| |
|
|
|
频率分布直方图如下:
(1)求频率分布表中所标字母的值,并补充完成频率分布直方图;
(2)若从身高属于第六组和第八组的所有男生中随机抽取 名男生,记他们的身高分别为
名男生,记他们的身高分别为 ,求满足:
,求满足: 的事件的概率.
的事件的概率.
在平面直角坐标系 中,动点
中,动点 满足:点
满足:点 到定点
到定点 与到
与到 轴的距离之差为
轴的距离之差为 .记动点
.记动点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2)过点 的直线交曲线
的直线交曲线 于
于 、
、 两点,过点
两点,过点 和原点
和原点 的直线交直线
的直线交直线 于点
于点 ,求证:直线
,求证:直线 平行于
平行于 轴.
轴.
 的展开式中,x的幂指数是整数的项共有
的展开式中,x的幂指数是整数的项共有 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,
, ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
. 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 时,过点
时,过点 的直线
的直线 交曲线
交曲线 于
于 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合), 试问:直线
不重合), 试问:直线 与
与 粤公网安备 44130202000953号
粤公网安备 44130202000953号