高中数学变量间的相关关系填空题

观察两相关量得如下数据:求两变量间的回归直线方程       ．

x	-1	-2	-3	-4	-5	5	3	4	2	1
y	-9	-7	-5	-3	-1	1	5	3	7	9

甲、乙两同学各自独立地考察两个变量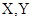的线性相关关系时,发现两人对 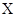的观察数据的平均值相等,都是,对的观察数据的平均值也相等,都是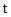,各自求出的回归直线分别是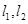,则直线与必过同一点____________

已知某回归直线过点，且样本数据中和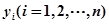的均值分别为
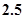和，则此回归直线方程为    .

调查了某地若干户家庭的年收入x（单位：万元）和年饮食支出y（单位：万元），调查显示年收入x与年饮食支出y具有线性相关关系，并由调查数据得到y对x的回归直线方程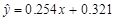：．由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加____________万元．

关于x与y，有如下数据

x	2	4	5	6	8
y	30	40	60	50	70

有如下的两个模型：①＝6.5x＋17.5，②＝7x＋17.通过残差分析发现第①个线性模型比第②个拟合效果好．则R________R，Q₁________Q₂.
(用大于，小于号填空，R，Q分别是相关指数和残差平方和)

下列关于回归分析的说法正确的是           （填上所有正确说法的序号）
①相关系数越小，两个变量的相关程度越弱；②残差平方和越大的模型，拟合效果越好；③用相关指数来刻画回归效果时，越小，说明模型的拟合效果越好；④用最小二乘法求回归直线方程，是寻求使取最小值时的的值；⑤在残差图中，残差点比较均匀地落在水平的带状区域内，说明选用的模型比较合适，这样的带状区域的宽度越窄，模型拟合精度越高.

下表是某厂1～4月份用水量(单位：百吨)的一组数据：

月份x	1	2	3	4
用水量y	4.5	4	3	2.5

由散点图可知，用水量y与月份x之间有较好的线性相关关系，其线性回归直线方程是y＝－0.7x＋a，则a等于________．

考古学家通过始祖鸟化石标本发现，其股骨长度（cm）与肱骨长度y(cm)线性
回归方程为，由此估计，当肌骨长度为50cm时，肱骨长度的估计值为
_____     cm.

某企业对自己的拳头产品的销售价格（单位：元）与月销售量（单位：万件）进行调查，其中最近五个月的统计数据如下表所示：

价格	9				11
销售量	11		8	6	5

由散点图可知，销售量与价格之间有较强的线性相关关系，其线性回归直线方程是：
，且，则＿＿＿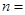

某工厂经过技术改造后，降低了能源消耗，经统计该厂某种产品的产量x(单位：吨)与相应的生产能耗y(单位：吨)有如下几组样本数据：

x	3	4	5	6
y	2.5	3	4	4.5

根据相关性检验，这组样本数据具有线性相关关系，通过线性回归分析，求得回归直线的斜率为0.7.已知该产品的年产量为10吨，则该工厂每年大约消耗的汽油为________吨．

数据x₁,x₂, …,x₈的平均数为6，标准差为2，则数据2x₁-6,2x₂-6, …,2x₈-6的平均数为___________，方差为_________.

对于有线性相关关系的变量x，y，测得一组数据如下表：

x	2	4	5	6	8
y	20	40	60	70	80

根据上表得它们的回归直线方程为，据此模型来预  测当x=20时，y的估计值为                

设有一个线性回归方程为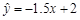，当变量增加一个单位时，y的值平均减少______

调查了某地若干户家庭的年收x（单位：万元）和年饮食支出y（单位：万元），调查显示年收入x与年饮食支出y具有线性相关关系，井由调查数据得到y对x的回归直线方程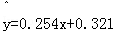．由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加      万元．

某产品在某零售摊位的零售价x（单位：元）与每天的销售量y（单位：个）的统计资料如下表所示：由上表可得回归直线方程中的，据此模型预测零售价为15元时，每天的销售量为             ．