高中数学变量间的相关关系填空题

在一项打鼾与患心脏病的调查中，共调查了2000人，经计算的=20.87，根据这一数据分析，我们有_______的把握认为打鼾与患心脏病是______ 的.

下表是某厂1～4月份用水量（单位：百吨）的一组数据，

月份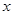	1	2	3	4
用水量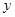	4.5	4	3	2.5

由其散点图可知，用水量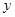与月份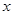之间有较好的线性相关关系，其线性回归方程是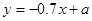，则=______________。

某新型企业随市场竞争加剧，为获取更大利润，企业须不断加大投资，若预计年利润率低于10%时，则该企业就考虑转型.下表显示的是某企业几年来年利润（百万）与年投资成本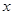（百万）变化的一组数据.

年份	2008	2009	2010	2011	…
投资成本x	3	5	9	17	…
年利润y	1	2	3	4	…

请你就以下4个函数模型
 


其中以下说法
A．           年投资成本与年利润正相关
B．            选择其适合的函数模型是
C．            若要使企业利润超过6百万，则该企业考虑转型.
你认为正确的是        （把你认为正确的都填上）

已知与之间的一组数据为

	0	1	2	3
	1	3	5	7

则与的回归直线方程必过定点________

已知x与y之间的一组数据：   

x	0	1	2	3
y	1	3	5	7

则y与x的线性回归方程为y=bx+a必过点           

已知x，y的取值如下表：

x	0	1	3	4
y	2.2	4.3	4.8	6.7

从散点图可以看出y与x线性相关，且回归方程为，则___________.

某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验．
根据收集到的数据（如下表），由最小二乘法求得回归方程．

现发现表中有一个数据模糊看不清，请你推断出该数据的值为       ．

下列说法中正确的是                    （填序号）
①回归分析就是研究两个相关事件的独立性；
②回归模型都是确定性的函数；
③回归模型都是线性的；
④回归分析的第一步是画散点图或求相关系数；
⑤回归分析就是通过分析、判断，确定相关变量之间的内在的关系的一种统计方法.

某大学在研究性别与职称(分正教授、副教授)之间是否有关系，你认为应该收集哪些数据？     ________ 

下列叙述中：
①变量间关系有函数关系，还有相关关系；②回归函数即用函数关系近似地描述相关关系；③；④线性回归方程一定可以近似地表示所有相关关系．
其中正确的有　　　　

已知在某种实践运动中获得一组数据，其中不慎将数据丢失，但知道这四组数据符合线性关系，则与a的近似值为    .

已知点所在的一组样本点的回归模型为，则该回归模型在处的残差为              。

已知x，Y之间的数据如下表所示，则Y与x之间的线性回归直线一定过点________.

x	1.08	1.12	1.19	1.28
Y	2.25	2.37	2.40	2.55

某数学老师身高176cm，他爷爷、父亲和儿子的身高分别是173cm、170cm和182cm．因儿子的身高与父亲的身高有关，该老师用线性回归分析的方法预测他孙子的身高为_____cm．

已知与之间的一组数据为

	0	1	2	3
	1	3	5-a	7+a

则与的回归直线方程必过定点___________；