某产品的广告费用x与销售额y的统计数据如下表
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39[ |
54 |
根据上表可得回归方程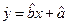 中的
中的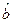 为9.4,据此模型预报广告费用为6万元时销售额为
为9.4,据此模型预报广告费用为6万元时销售额为
A.63.6万元 B.65.5万元 C.67.7万元 D
D .72.0万元
.72.0万元
一项研究要确定是否能够根据施肥量预测作物的产量。这里的预报释变量是( )
| A.作物的产量 | B.施肥量 |
| C.试验者 | D.降雨量或其他解释产量的变量 |
通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
| |
男 |
女 |
总计 |
| 爱好 |
40 |
20 |
60 |
| 不爱好 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
由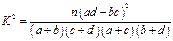 算得,
算得,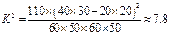 .
.
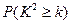 |
0.050 |
0.010 |
0.001 |
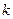 |
3.841 |
6.635 |
10.828 |
参照附表,得到的正确结论是( )
A.再犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.再犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
若由资料可知y对x呈线性相关关系,则y与x的线性回归方程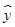 =bx+a必过的点是
=bx+a必过的点是
| A.(2,2) | B.(1,2) | C.(3,4) | D.(4,5) |
已知变量 呈线性相关关系,回归方程为
呈线性相关关系,回归方程为 ,则变量
,则变量 是( )
是( )
| A.线性正相关关系 | B.由回归方程无法判断其正负相关 |
| C.线性负相关关系 | D.不存在线性相关关系 |
容量为100的样本数据,按从小到大的顺序分为8组,如下表:
第三组的频数和频率分别是 ( )
A. 和0.14 和0.14 |
B.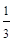 和 和 |
C.14和0.14 | D.0.14和14 |
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了下表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
20 |
5 |
25 |
| 女生 |
10 |
15 |
25 |
| 合计 |
30 |
20 |
50 |
则根据表中的数据,计算随机变量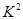 的值,并参考有关公式,你认为性别与是否喜爱打篮球之间有关系的把握有
的值,并参考有关公式,你认为性别与是否喜爱打篮球之间有关系的把握有
A.0 B.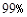 C .99.5% D.
C .99.5% D.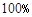
调查某医院某段时间内婴儿出生的时间与性别的关系,由 列联表得出
列联表得出 ,故有 把握认为婴儿的性别与出生时间有关系(利用下表解决问题)( )
,故有 把握认为婴儿的性别与出生时间有关系(利用下表解决问题)( )
A. |
B. |
C. |
D. |
为研究变量 的线性相关性,甲、乙二人分别作了研究,利回线性回归方法
的线性相关性,甲、乙二人分别作了研究,利回线性回归方法
得到回归直线方程 ,两人计算知
,两人计算知 相同,
相同, 也相同,下列正确的是( )
也相同,下列正确的是( )
A. 重合 重合 |
B. 一定平行 一定平行 |
C. |
D.无法判断 是否相交 是否相交 |
在一次实验中,采集到如下一组数据:
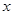 |
-2.0 |
-1.0 |
0 |
1.00 |
2.00 |
3.00 |
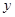 |
0.24 |
0.51 |
1 |
2.02 |
3.98 |
8.02 |
则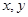 的函数关系与下列( )类函数最接近(其中
的函数关系与下列( )类函数最接近(其中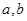 为待定系数)
为待定系数)
A.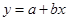 B .
B .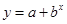 C.
C.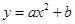 D.
D.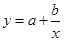
有五组变量:
①汽车的重量和汽车每消耗1升汽油所行驶的平均路程;
②平均日学习时间和平均学习成绩;
③某人每日吸烟量和其身体健康情况;
④正方形的边长和面积; 
⑤汽车的重量和百公里耗油量;
其中两个变量成正相关关系的是
| A.①③ | B.②④ | C.②⑤ | D.④⑤ |
某产品的广告费用
与销售额
的统计数据如下表:
| 广告费用
(万元) |
4 |
2 |
3 |
5 |
| 销售额
(万元) |
49 |
26 |
39 |
54 |
根据上表可得回归方程
中的
为9.4,据此模型预报广告费用为6万元时销售额为
| A. | 63.6万元 |
B. | 65.5万元 |
C. | 67.7万元 |
D. | 72.0万元 |
若某地财政收入x与支出y满足线性回归方程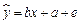 (单位:亿元),其中b=0.8,a=2,|e|<0.5,如果今年该地区财政收入10亿元,年支出预计不会超过( )
(单位:亿元),其中b=0.8,a=2,|e|<0.5,如果今年该地区财政收入10亿元,年支出预计不会超过( )
| A.10亿元 | B.9亿元 | C.10.5亿元 | D.9.5亿元 |
对于事件A和事件B,通过计算得到K2的观测值k≈4.514,下列说法正确的是( )
| A.有99%的把握说事件A和事件B有关 |
| B.有95%的把握说事件A和事件B有关 |
| C.有99%的把握说事件A和事件B无关 |
| D.有95%的把握说事件A和事件B无关 |