甲、乙、丙、丁四位同学各自对A、B两变量的线性相关性作试验,并用回归分析方法分别求得相关系数r与残差平方和m如下表;则哪位同学的试验结果体现A、B两变量更强的线性相关性
A.丁 B.丙 C.乙 D.甲
| |
甲 |
乙 |
丙 |
丁 |
| r |
0.82 |
0.78 |
0.69 |
0.85 |
| m |
115 |
106 |
124 |
103 |
下列关系中,具有相关关系的是( )
| A.人的身高与体重; | B.匀速行驶的车辆所行驶距离与行驶的时间; |
| C.人的身高与视力; | D.正方体的体积与边长。 |
右面是一个2×2列联表,则表中 处的值分别为( )
处的值分别为( )
| |
 |
 |
总计 |
 |
 |
25 |
73 |
 |
21 |
 |
 |
| 总计 |
 |
49 |
|
A. 98, 28
B. 28, 98
C. 48, 45
D. 45, 48
某商品销售量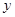 (件)与销售价格
(件)与销售价格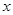 (元/件)负相关,则其回归方程可能是( )
(元/件)负相关,则其回归方程可能是( )
A. =-10x+200 =-10x+200 |
B. =10x+200 =10x+200 |
C. =-10x-200 =-10x-200 |
D. =10x-200 =10x-200 |
关于相关系数r,下列说法中正确的有:
①若 ,则
,则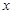 增大时,
增大时, 也相应增大;
也相应增大;
②若 ,则
,则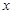 增大时,
增大时, 也相应增大;
也相应增大;
③若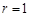 ,或
,或 ,则
,则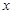 与
与 的关系完全对应(有函数关系),在散点图上各个散点均在一条直线上.( )
的关系完全对应(有函数关系),在散点图上各个散点均在一条直线上.( )
| A.①② | B.②③ | C.①③ | D.①②③ |
有下列说法:①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适.②相关指数R2来刻画回归的效果, R2值越大,说明模型的拟合效果越好.③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型,拟合效果越好.其中正确命题的个数是 ( )
| A.0 | B.1 | C.2 | D.3 |
下面两个变量间的关系是相关关系的是( )
| A.正方体的棱长与体积 |
| B.角的度数与它的正弦值 |
| C.单产为常数时,土地面积与粮食总产量 |
| D.日照时间与水稻的亩产量 |
某产品的广告费用x与销售额y的统计数据如下表
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39 |
54 |
根据上表可得回归方程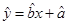 中的
中的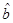 为9.4,据此模型预报广告费用为6万元时销售额为 ( )
为9.4,据此模型预报广告费用为6万元时销售额为 ( )
A.63.6万元 B.65.5万元 C.67.7万元 D.72.0万元
某学生四次模拟考试时,其英语作文的减分情况如下表:
| 考试次数x |
1 |
2 |
3 |
4 |
| 所减分数y |
4.5 |
4 |
3 |
2.5 |
显然所减分数y与模拟考试次数x之间有较好的线性相关关系,则其线性回归方程为
A.
B.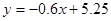
C.
D.
下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗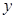 (吨)的几组对应数据:
(吨)的几组对应数据:
 |
3 |
4 |
5 |
6 |
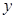 |
2.5 |
 |
4 |
4.5 |
根据上表提供的数据,求出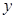 关于
关于 的线性回归方程为
的线性回归方程为 ,那么表中
,那么表中 的值为
的值为
A、4.5
B、3.5
C、3.15
D、3
一组数据12,15,24,25,31,31,36,36,37,39,44,49,50的中位数是 ( )
A 36 B 31 C 35 D 34
下列关系属负相关的是( )
A 父母的身高与子女身高的关系 B 农作物产量与施肥的关系
C 吸烟与健康的关系 D 数学成绩与物理成绩的关系