在一次考试中,5名同学数学、物理成绩如下表所示:
| 学生 |
A |
B |
C |
D |
E |
| 数学(x分) |
89 |
91 |
93 |
95 |
97 |
| 物理(y分) |
87 |
89 |
89 |
92 |
93 |
(1)根据表中数据,求物理分 对数学分
对数学分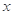 的回归方程:
的回归方程:
(2)要从4名数学成绩在90分以上的同学中选出2名参加一项活动,以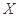 表示选中的同学中物理成绩高于90分的人数,求随机变量
表示选中的同学中物理成绩高于90分的人数,求随机变量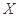 的分布列及数学期望
的分布列及数学期望 .(附:回归方程
.(附:回归方程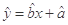 中,
中,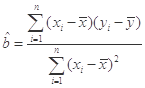 ,
, )
)
以下四个命题中:
①在回归分析中,可用相关指数 的值判断模型的拟合效果,
的值判断模型的拟合效果,  越大,模型的拟合效果越好;
越大,模型的拟合效果越好;
②两个随机变量的线性相关性越强,相关系数的绝对值越接近于1;
③若数据 的方差为1,则
的方差为1,则 的方差为2;
的方差为2;
④对分类变量与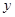 的随机变量
的随机变量 的观测值
的观测值 来说,
来说, 越小,判断“
越小,判断“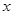 与
与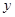 有关系”的把握程度越大.
有关系”的把握程度越大.
其中真命题的个数为( )
| A.1 | B.2 | C.3 | D.4 |
如图是某班 为学生期中考试数学成绩的频率分布直方图,其中成绩分组区间是:
为学生期中考试数学成绩的频率分布直方图,其中成绩分组区间是: ,
, ,
, ,
, ,
, ,
, ,则图中
,则图中 的值等于( )
的值等于( )
A. |
B. |
C. |
D. |
在一个2×2列联表中,由其数据计算得到K2的观测值k=13.097,则其两个变量间有关系的可能性为( )
| A.99.9% | B.95% | C.90% | D.0 |
附表:
 |
0.050 |
0.010 |
0.001 |
| k |
3.841 |
6.635 |
10.828 |
欲知作者的性别是否与读者的性别有关,某出版公司派人员到各书店随机调查了500位买书的顾客,结果如下:
| 作家 读者 |
男作家 |
女作家 |
合计 |
| 男读者 |
142 |
122 |
264 |
| 女读者 |
103 |
133 |
236 |
| 合计 |
245 |
255 |
500 |
则作者的性别与读者的性别 (填“有关”或“无关”)。
(本小题满分12分)某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 (个) (个) |
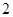 |
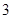 |
 |
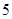 |
加工的时间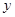 (小时) (小时) |
 |
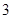 |
 |
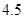 |
(1)在给定的坐标系中画出表中数据的散点图;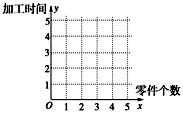
(2)求出 关于
关于 的线性回归方程
的线性回归方程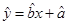 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工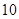 个零件需要多少时间?
个零件需要多少时间?
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如图所示,则下列结论错误的一个是( )
| A.甲的极差是29 | B.乙罚球比甲更稳定 |
| C.甲罚球的命中率比乙高 | D.甲的中位数是24 |
(本小题满分12分)为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x(单位:小时)与当天投篮命中率y之间的关系:
| 时间x |
1 |
2 |
3 |
4 |
5 |
| 命中率y |
0.4 |
0.5 |
0.6 |
0.6 |
0.4 |
(1)求小李这5天的平均投篮命中率;
(2)用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.
某次测量发现一组数据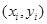 具有较强的相关性,并计算得
具有较强的相关性,并计算得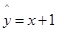 ,其中数据
,其中数据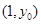 ,Y)因书写不清,只记得
,Y)因书写不清,只记得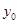 是[0,3]内的任意一个值,则该数据对应的残差的绝对值不大于l的概率为__________.(残差=真实值一预测值)
是[0,3]内的任意一个值,则该数据对应的残差的绝对值不大于l的概率为__________.(残差=真实值一预测值)
某次测量发现一组数据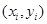 具有较强的相关性,并计算得
具有较强的相关性,并计算得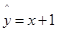 ,其中数据
,其中数据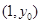 ,Y)因书写不清,只记得
,Y)因书写不清,只记得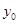 是[0,3]内的任意一个值,则该数据对应的残差的绝对值不大于l的概率为__________.(残差=真实值一预测值)
是[0,3]内的任意一个值,则该数据对应的残差的绝对值不大于l的概率为__________.(残差=真实值一预测值)
从某高中随机选取5名高二男生,其身高和体重的数据如下表所示:
| 身高 x(cm) |
160 |
165 |
170 |
175 |
180 |
| 体重y(kg) |
63 |
66 |
70 |
72 |
74 |
由表可得回归直线方程 ,据此模型预报身高为
,据此模型预报身高为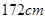 的男生的体重大约为( )
的男生的体重大约为( )
A.70.09kg B.70.12kg C.70.55kg D.71.05kg
已知某企业上半年前5个月产品广告投入与利润额统计如下:
| 月份 |
1 |
2 |
3 |
4 |
5 |
| 广告投入(x万元) |
9.5 |
9.3 |
9.1 |
8.9 |
9.7 |
| 利润(y万元) |
92 |
89 |
89 |
87 |
93 |
由此所得回归方程为 ,若6月份广告投入10万元,估计所获得利润为( )
,若6月份广告投入10万元,估计所获得利润为( )
A.95.25万元 B.96.5万元 C.97万元 D.97.25万元