某地最近十年粮食需求量逐年上升,下表是部分统计数据:
| 年份 |
2002 |
2004 |
2006 |
2008 |
2010 |
| 需求量(万吨) |
236 |
246 |
257 |
276 |
286 |
(Ⅰ)利用所给数据求年需求量与年份之间的回归直线方程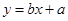 ;
;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地2012年的粮食需求量.
一次考试中,五名学生的数学、物理成绩如下表所示:
| 学生 |
A1 |
A2 |
A3 |
A4 |
A5 |
| 数学(x分) |
89 |
91 |
93 |
95 |
97 |
| 物理(y分) |
87 |
89 |
89 |
92 |
93 |
(1)请在所给的直角坐标系中画出它们的散点图
(2)并求这些数据的线性回归方程 =bx+a.
=bx+a.
附:线性回归方程 中,
中,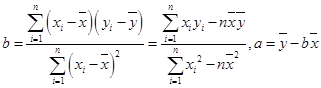
其中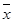 ,
, 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为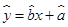 .
.
一名小学生的年龄和身高(单位:cm)的数据如下表:

由散点图可知,身高y与年龄x之间的线性回归方程为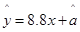 ,预测该学生10岁时的身高为( )
,预测该学生10岁时的身高为( )
| A.154 | B.153 | C.152 | D.151 |
某地区2008年至2014年农村居民家庭纯收入y(单位:千元)的数据如下表:
| 年份 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
2014 |
年份代号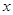 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 人均纯收入y |
2.9 |
3.3 |
3.6 |
4.4 |
4.8 |
5.2 |
5.9 |
(Ⅰ)求y关于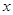 的线性回归方程;
的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2008年至2014年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2016年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: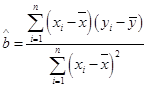 ,
, .
.
(本小题满分12分)
从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得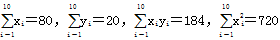 .
.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中,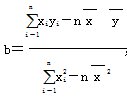 ,a=
,a= -b
-b 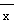 ,其中
,其中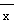 ,
, 为样本平均值.
为样本平均值.
在某条件下的汽车测试中,驾驶员在一次加满油后的连续行驶过程中从汽车仪表盘得到如下信息:
| 时间 |
油耗(升/100公里) |
可继续行驶距离(公里) |
| 10:00 |
9.5 |
300 |
| 11:00 |
9.6 |
220 |
注: ,
,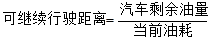 ,
,
 .
.
从以上信息可以推断在10:00—11:00这一小时内 (填上所有正确判断的序号).
行驶了80公里;
行驶不足80公里;
平均油耗超过9.6升/100公里;
平均油耗恰为9.6升/100公里;
平均车速超过80公里/小时.
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.根据收集到的数据(如下表),由最小二乘法示得回归直线方程为 。
。
零件数 (个) (个) |
10 |
20 |
30 |
40 |
50 |
加工时间 |
62 |
|
75 |
81 |
89 |
表中有一个数据模糊不清,经推断,该数据的值为 .
表中提供了某厂节能降耗技术改造后生产 产品过程中记录的产量
产品过程中记录的产量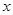 (吨)与相应的生产能耗
(吨)与相应的生产能耗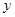 (吨标准煤)的几组对应数据.根据下表提供的数据,求出
(吨标准煤)的几组对应数据.根据下表提供的数据,求出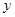 关于
关于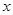 的线性回归方程为
的线性回归方程为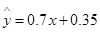 ,那么表中
,那么表中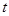 的值为( )
的值为( )
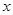 |
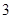 |
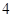 |
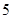 |
 |
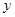 |
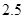 |
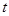 |
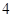 |
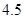 |
A.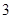 B.
B.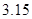 C.
C.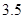 D.
D.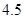
(本小题满分18分)某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温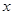 (°C)与该奶茶店的这种饮料销量
(°C)与该奶茶店的这种饮料销量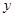 (杯),得到如下数据:
(杯),得到如下数据:
| 日 期 |
1月11日 |
1月12日 |
1月13日 |
1月14日 |
1月15日 |
平均气温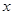 (°C) (°C) |
9 |
10 |
12 |
11 |
8 |
销量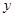 (杯) (杯) |
23[] |
25 |
30 |
26 |
21 |
(1)若从这五组数据中随机抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出y关于x的线性回归方程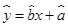 .
.
(参考公式: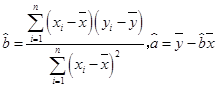 .)
.)
在西非肆虐的“埃博拉病毒”的传播速度很快,这已经成为全球性的威胁.为了考察某种埃博拉病毒疫苗的效果,现随机抽取100只小鼠进行试验,得到如下列联表:

参照附表,下列结论正确的是( ).
A.在犯错误的概率不超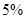 过的前提下,认为“小动物是否被感染与有没有服用疫苗有关”; 过的前提下,认为“小动物是否被感染与有没有服用疫苗有关”; |
B.在犯错误的概率不超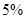 过的前提下,认为“小动物是否被感染与有没有服用疫苗无关”; 过的前提下,认为“小动物是否被感染与有没有服用疫苗无关”; |
C.有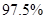 的把握认为“小动物是否被感染与有没有服用疫苗有关”; 的把握认为“小动物是否被感染与有没有服用疫苗有关”; |
D.有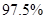 的把握认为“小动物是否被感染与有没有服用疫苗无关”. 的把握认为“小动物是否被感染与有没有服用疫苗无关”. |
已知具有线性相关的两个变量x,y之间的一组数据如下:
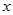 |
0 |
1 |
2 |
3 |
4 |
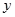 |
2.2 |
4.3 |
t |
4.8 |
6.7 |
且回归方程是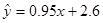 ,则t=( )
,则t=( )
A.2.5 B.3.5 C.4.5 D.5.5
登山族为了了解某山高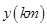 与气温
与气温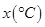 之间的关系,随机统计了4次山高与相应的气温,并制作了对照表:
之间的关系,随机统计了4次山高与相应的气温,并制作了对照表:
| 气温x(°C) |
18 |
13 |
10 |
-1 |
| 山高y(km) |
24 |
34 |
38 |
64 |
由表中数据,得到线性回归方程
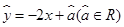 ,由此请估计出山高为72(km)处气温的度数为( )
,由此请估计出山高为72(km)处气温的度数为( )
A.-10 B.-8 C.-4 D.-6
已知关于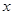 与
与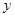 之间的一组数据:
之间的一组数据:
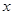 |
2 |
3 |
3 |
6 |
6 |
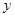 |
2 |
6 |
6 |
10 |
11 |
则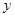 与
与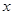 的线性回归方程
的线性回归方程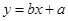 必过点( )
必过点( )
A.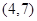 B.
B.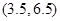 C.
C.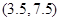 D.
D.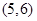
观察分析下表中的数据:
| 多面体 |
面数(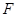 ) ) |
顶点数(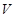 ) ) |
棱数(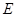 ) ) |
| 三棱锥 |
5 |
6 |
9 |
| 五棱锥 |
6 |
6 |
10 |
| 立方体] |
6 |
8 |
12 |
猜想一般凸多面体中,面数、顶点数、棱数: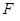 、
、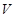 、
、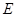 所满足的等式是 .
所满足的等式是 .