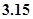下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程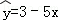 ,变量x增加一个单位时,y平均增加5个单位;
,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程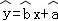 必过(
必过( );
);
④在一个2×2列联中,由计算得K2=13.079则有99%的把握确认这两个变量间有关系;
其中错误 的个数是( ).
本题可以参考独立性检验临界值表:
| P(K2≥k) |
0.5 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.25 |
0.010 |
0.005 |
0.001 |
| k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.535 |
7.879 |
10.828 |
A.0 B.1 C.2 D.3
如果随机变量ξ~B(n,p),且Eξ=7,Dξ=6,则P等于_________ .
某车间加工零件的数量 与加工时间
与加工时间 的统计如下表:
的统计如下表:
零件数 (个) (个) |
10 |
20 |
30 |
加工时间 (分钟) (分钟) |
21 |
30 |
39 |
现已求得上表数据的回归方程 中的值
中的值 为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( ).
为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( ).
A.84分钟 B.94分钟 C.102分钟 D.112分钟
假设关于某设备的使用年限 和所支出的维修费用
和所支出的维修费用 (万元),有如下的统计资料:
(万元),有如下的统计资料:
使用年限 |
2 |
3 |
4 |
5 |
6 |
维修费用 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料知道 对
对 呈线性相关关系.
呈线性相关关系.
附:
试求:
(1)线性回归方程 的回归系数.
的回归系数.
(2)估计使用年限为10年时,维修费用是多少?
设有一个直线回归方程为 ,则变量
,则变量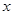 增加一个单位( )
增加一个单位( )
| A.y平均增加 1.5 个单位 |
| B.y 平均增加 2 个单位 |
| C.y 平均减少 1.5 个单位 |
| D.y 平均减少 2 个单位 |
有人收集了春节期间平均气温x(℃)与某取暖商品销售额y(万元)的有关数据(x,y)分别为:(﹣2,20),(﹣3,23),(﹣5,27),(﹣6,30),根据以上数据,用线性回归的方法,求得销售额y与平均气温x之间线性回归方程y=bx+a的系数b=﹣2.4,则预测平均气温为﹣8℃时该商品的销售额为_________ 万元.
某小卖部销售一品牌饮料的零售价x(元/评)与销售量y(瓶)的关系统计如下:
| 零售价x(元/瓶) |
3.0 |
3.2 |
3.4 |
3.6 |
3.8 |
4.0 |
| 销量y(瓶) |
50 |
44 |
43 |
40 |
35 |
28 |
已知的关系符合线性回归方程,其中.当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
A.20 B.22 C.24 D.26
下列五个命题
①任何两个变量都具有相关关系 ②圆的周长与该圆的半径具有相关关系
③某商品的需求量与该商品的价格是一种非确定性关系
④根据散点图求得的回归直线方程可能是没有意义的
⑤两个变量间的相关关系可以通过回归直线,把非确定性问题转化为确定性问题进行研究
正确命题的序号为____________.
已知某企业上半年前5个月产品广告投入与利润额统计如下:
| 月份 |
1 |
2 |
3 |
4 |
5 |
| 广告投入(x万元) |
9.5 |
9.3 |
9.1 |
8.9 |
9.7 |
| 利润(y万元) |
92 |
89 |
89 |
87 |
93 |
由此所得回归方程为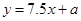 ,若6月份广告投入10(万元)估计所获利润为( )
,若6月份广告投入10(万元)估计所获利润为( )
A.95.25万元 B.96.5万元 C.97万元 D.97.25万元
已知x与y之间的一组数据:
| x |
0 |
1 |
2 |
3 |
| y |
1 |
3 |
5 |
7 |
则y与x的线性回归方程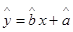 必过点( )
必过点( )
A.(1.5 ,4) B.(2,2) C.(1.5 ,0) D.(1,2)
已知x与y之间的一组数据:
| x |
0 |
1 |
2 |
3 |
| y |
1 |
3 |
5 |
7 |
则y与x的线性回归方程为 必过点( )
必过点( )
A .(2,2) B. (1.5 ,4) C.(1.5 ,0) D.(1,2)
对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( ).
| A.r2<r4<0<r3<r1 | B.r4<r2<0<r1<r3 | C.r4<r2<0<r3<r1 | D.r2<r4<0<r1<r3 |
在2014年3月15日,某超市对某种商品的销售量及其售价进行调查分析,发现售价x元和销售量y件之间的一组数据如下表所示:
| 售价x |
9 |
9.5 |
10 |
10.5 |
11 |
| 销售量y |
11 |
10 |
8 |
6 |
5 |
由散点图可知,销售量y与售价x之间有较好的线性相关关系,其线性回归方程是:y= -3.2x+a,则a=( )
A.-24 B.35.6 C.40.5 D.40
某车间加工零件的数量 与加工时间
与加工时间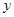 的统计数据如下表:
的统计数据如下表:
零件数 (个) (个) |
10 |
20 |
30 |
加工时间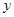 (分钟) (分钟) |
21 |
30 |
39 |
现已求得上表数据的回归方程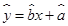 中的
中的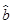 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
A.84分钟 B.94分钟 C.102分钟 D.112分钟
下表提供了某厂节能降耗技术改造后生产某产品过程中记录的产量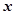 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨)的几组对应数据. 根据表中提供的数据,求出
(吨)的几组对应数据. 根据表中提供的数据,求出 关于
关于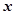 的线性回归方程是
的线性回归方程是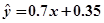 ,那么表中
,那么表中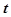 的值是( )
的值是( )
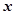 |
3 |
4 |
5 |
6 |
 |
2.5 |
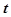 |
4 |
4.5 |
A.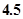 B.
B.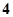 C.
C.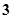 D.
D.