设某中学的女生体重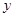 (kg)与身高
(kg)与身高 (cm)具有线性相关关系,根据一组样本数
(cm)具有线性相关关系,根据一组样本数
 ,用最小二乘法建立的线性回归直线方程为
,用最小二乘法建立的线性回归直线方程为 ,给出下列结论,则错误的是( )
,给出下列结论,则错误的是( )
A.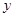 与 与 具有正的线性相关关系 具有正的线性相关关系 |
| B.若该中学某女生身高增加1cm,则其体重约增加0.85kg |
C.回归直线至少经过样本数据  中的一个 中的一个 |
D.回归直线一定过样本点的中心点 |
对变量 ,
,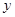 观测数据
观测数据 ,得散点图
,得散点图 ;对变量
;对变量 ,
, 有观测数据
有观测数据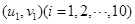 ,得散点图
,得散点图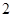 .由这两个散点图可以判断( )
.由这两个散点图可以判断( )

A.变量 与 与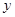 正相关, 正相关, 与 与 正相关 正相关 |
B.变量 与 与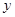 正相关, 正相关, 与 与 负相关 负相关 |
C.变量 与 与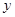 负相关, 负相关, 与 与 正相关 正相关 |
D.变量 与 与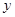 负相关, 负相关, 与 与 负相关 负相关 |
在一次数学实验中,运用计算器采集到如下一组数据:
| x |
-2.0 |
-1.0 |
0 |
1.00 |
2.00 |
3.00 |
| y |
0.24 |
0.51 |
1 |
2.02 |
3.98 |
8.02 |
则x,y的函数关系与下列哪类函数最接近(其中,a,b为待定系数)( )
A.y=a+bx B.y=a+bx
C.y=a+logbx D.y=a+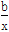
一名小学生的年龄和身高(单位:cm)的数据如下表:

由散点图可知,身高y与年龄x之间的线性回归方程为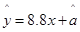 ,预测该学生10岁时的身高为( )
,预测该学生10岁时的身高为( )
| A.154 | B.153 | C.152 | D.151 |
表中提供了某厂节能降耗技术改造后生产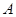 产品过程中记录的产量
产品过程中记录的产量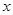 (吨)与相应的生产能耗
(吨)与相应的生产能耗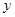 (吨标准煤)的几组对应数据.根据下表提供的数据,求出
(吨标准煤)的几组对应数据.根据下表提供的数据,求出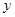 关于
关于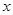 的线性回归方程为
的线性回归方程为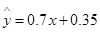 ,那么表中
,那么表中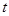 的值为( )
的值为( )
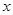 |
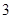 |
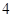 |
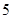 |
 |
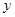 |
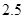 |
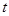 |
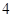 |
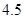 |
A.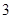 B.
B.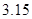 C.
C.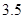 D.
D.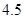
在西非肆虐的“埃博拉病毒”的传播速度很快,这已经成为全球性的威胁.为了考察某种埃博拉病毒疫苗的效果,现随机抽取100只小鼠进行试验,得到如下列联表:

参照附表,下列结论正确的是( ).
A.在犯错误的概率不超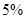 过的前提下,认为“小动物是否被感染与有没有服用疫苗有关”; 过的前提下,认为“小动物是否被感染与有没有服用疫苗有关”; |
B.在犯错误的概率不超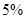 过的前提下,认为“小动物是否被感染与有没有服用疫苗无关”; 过的前提下,认为“小动物是否被感染与有没有服用疫苗无关”; |
C.有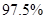 的把握认为“小动物是否被感染与有没有服用疫苗有关”; 的把握认为“小动物是否被感染与有没有服用疫苗有关”; |
D.有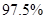 的把握认为“小动物是否被感染与有没有服用疫苗无关”. 的把握认为“小动物是否被感染与有没有服用疫苗无关”. |
已知具有线性相关的两个变量x,y之间的一组数据如下:
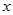 |
0 |
1 |
2 |
3 |
4 |
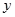 |
2.2 |
4.3 |
t |
4.8 |
6.7 |
且回归方程是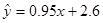 ,则t=( )
,则t=( )
A.2.5 B.3.5 C.4.5 D.5.5
登山族为了了解某山高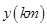 与气温
与气温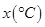 之间的关系,随机统计了4次山高与相应的气温,并制作了对照表:
之间的关系,随机统计了4次山高与相应的气温,并制作了对照表:
| 气温x(°C) |
18 |
13 |
10 |
-1 |
| 山高y(km) |
24 |
34 |
38 |
64 |
由表中数据,得到线性回归方程
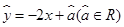 ,由此请估计出山高为72(km)处气温的度数为( )
,由此请估计出山高为72(km)处气温的度数为( )
A.-10 B.-8 C.-4 D.-6
已知关于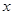 与
与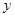 之间的一组数据:
之间的一组数据:
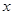 |
2 |
3 |
3 |
6 |
6 |
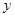 |
2 |
6 |
6 |
10 |
11 |
则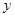 与
与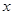 的线性回归方程
的线性回归方程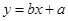 必过点( )
必过点( )
A.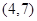 B.
B.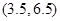 C.
C.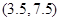 D.
D.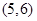
某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系,随机抽查52名中学生,得到统计数据如表1至表4,这与性别有关联的可能性最大的变量是( )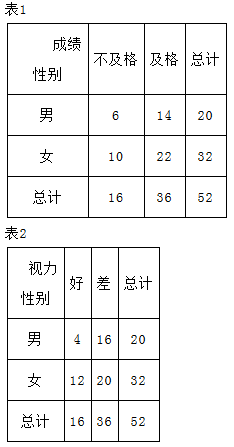
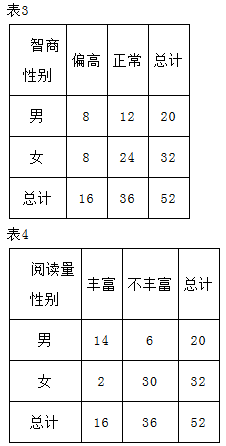
| A.成绩 | B.视力 | C.智商 | D.阅读量 |
对于函数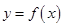 ,部分
,部分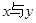 的对应关系如下表:
的对应关系如下表:
数列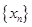 满足:
满足: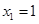 ,且对于任意
,且对于任意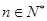 ,点
,点 都在函数
都在函数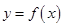 的图象上,则
的图象上,则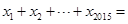 ( )
( )
| A.7539 | B.7546 | C.7549 | D.7554 |