山东省日照市高三校际联合检测(二模)文科数学试卷
在复平面内,复数 (i是虚数单位)对应的点在( )
(i是虚数单位)对应的点在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
采用系统抽样方法从1000人中抽取50人做问卷调查,为此将他们随机编号1,, ,1000,适当分组后在第一组采用简单随机抽样的方法抽到的号码为8,抽到的50人中,编号落入区间 的人做问卷A,编号落入区间
的人做问卷A,编号落入区间 的人做问卷B,其余的人做问卷C,则抽到的人中,做问卷C的人数为( )
的人做问卷B,其余的人做问卷C,则抽到的人中,做问卷C的人数为( )
| A.12 | B.13 | C.14 | D.15 |
下列说法不正确的是( )
| A.若“p且q”为假,则p,q至少有一个是假命题 |
B.命题“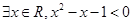 ”的否定是“ ”的否定是“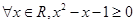 ” ” |
C.“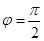 ”是“ ”是“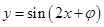 为偶函数”的充要条件 为偶函数”的充要条件 |
D.当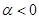 时,幂函数 时,幂函数 上单调递减 上单调递减 |
将函数 的图象上各点的纵坐标不变,横坐标扩大到原来的2倍,所得图象的一条对称轴方程可以是( )
的图象上各点的纵坐标不变,横坐标扩大到原来的2倍,所得图象的一条对称轴方程可以是( )
A. |
B. |
C. |
D. |
变量 满足线性约束条件
满足线性约束条件 目标函数
目标函数 仅在点
仅在点 取得最小值,则k的取值范围是( )
取得最小值,则k的取值范围是( )
A. |
B. |
C. |
D. |
对于函数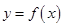 ,部分
,部分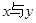 的对应关系如下表:
的对应关系如下表:
数列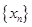 满足:
满足: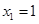 ,且对于任意
,且对于任意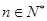 ,点
,点 都在函数
都在函数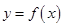 的图象上,则
的图象上,则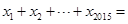 ( )
( )
| A.7539 | B.7546 | C.7549 | D.7554 |
在平面直角坐标系 中,设直线
中,设直线 与圆
与圆 交于A,B两点,O为坐标原点,若圆上一点C满足
交于A,B两点,O为坐标原点,若圆上一点C满足 ,则r=______.
,则r=______.
(本小题满分12分)在 中,已知
中,已知 .
.
(Ⅰ)求sinA与角B的值;
(Ⅱ)若角A,B,C的对边分别为 的值.[
的值.[
(本小题满分12分)某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组 ,第二组
,第二组 , ,第五组
, ,第五组 .右图是按上述分组方法得到的频率分布直方图.
.右图是按上述分组方法得到的频率分布直方图.
按上述分组方法得到的频率分布直方图.
(Ⅰ)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(Ⅱ)设m,n表示该班某两位同学的百米测试成绩,且已知 求事件“
求事件“ ”发生的概率.
”发生的概率.
(本小题满分12分) 是边长为4的等边三角形,
是边长为4的等边三角形, 是等腰直角三角形,
是等腰直角三角形, ,平面
,平面 平面ABD,且
平面ABD,且 平面ABC,EC=2.
平面ABC,EC=2.
(Ⅰ)证明:DE//平面ABC;
(Ⅱ)证明: .
.
(本小题满分12分)已知数列 的前
的前 项和为
项和为 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设集合 ,等差数列
,等差数列 的任一项
的任一项 ,其中
,其中 是
是 中的最小数,
中的最小数, ,求数列
,求数列 的通项公式.
的通项公式.
(本小题满分13分)已知以C为圆心的动圆过定点 ,且与圆
,且与圆 (B为圆心)相切,点C的轨迹为曲线T.设Q为曲线T上(不在x轴上)的动点,过点A作OQ(O为坐标原点)的平行线交曲线T于M,N两点.
(B为圆心)相切,点C的轨迹为曲线T.设Q为曲线T上(不在x轴上)的动点,过点A作OQ(O为坐标原点)的平行线交曲线T于M,N两点.
(Ⅰ)求曲线T的方程;
(Ⅱ)是否存在常数 ,使
,使 总成立?若存在,求
总成立?若存在,求 ;若不存在,说明理由.
;若不存在,说明理由.
 ( )
( )



 (e是自然对数的底数)的部分图象大致是( )
(e是自然对数的底数)的部分图象大致是( )

 的所有零点之和为( )
的所有零点之和为( ) 的值是_________.
的值是_________. 的左焦点
的左焦点 ,右焦点
,右焦点 ,离心率
,离心率 .若点P为双曲线C右支上一点,则
.若点P为双曲线C右支上一点,则 __________.
__________.
 满足
满足 ,则
,则 的最小值为________.
的最小值为________. ..
.. ,求函数
,求函数 的最大值;
的最大值; ,求函数
,求函数 的单调区间;
的单调区间; ,正实数
,正实数 满足
满足 ,证明
,证明 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号