高中数学随机抽样试题

海关对同时从三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量（单位：件）如右表所示，工作人员用分层抽样的方法从这些商品中共抽取6件进行检测

地区
数量	50	150	100

（1）求这6件样品中来自各地区商品的数量；
（2）若在这6件样品中随机抽取2件送往甲机构进一步检测，求这2件商品来自相同地区的概率.

某中学将100名高一新生分成水平相同的甲，乙两个“平行班”，每班50人.陈老师采用A,B两种不同的教学方式分别在甲，乙两个班级进行教改实验.为了解教学效果，期末考试后，陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计，作出茎叶图如下，计成绩不低于90分者为“成绩优秀”.

（1）从乙班样本的20个个体中，从不低于86分的成绩中随机抽取2个，求抽出的两个均“成绩优秀”的概率；
（2）由以上统计数据填写下面2x2列联表，并判断是否有的把握认为“成绩优秀”与教学方式有关.

	甲班（A方式）	乙班（B方式）	总计
成绩优秀
成绩不优秀
总计

附：

P（	0.25	0.15	0.10	0.05	0.025
k	1.323	2.072	2.706	3.841	5.024

某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组得到的频率分布表如下图所示，

班号	分组	频数	频率
第1组		5	0.050
第2组		①	0.350
第3组		30	②
第4组		20	0.200
第5组		10	0.100
合计	100	1.00

（1）请先求出频率分布表中①、②位置相应的数据，再在答题纸上完成下列频率分布直方图；
（2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试？
（3）在（2）的前提下，学校决定在6名学生中随机抽取2名学生接受A考官的面试，求：第4组至少有一名学生被考官A面试的概率？

某公司生产产品A，产品质量按测试指标分为：指标大于或等于90为一等品，大于或等于小于为二等品，小于为三等品，生产一件一等品可盈利50元，生产一件二等品可盈利元，生产一件三等品亏损10元．现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测，检测结果统计如下：

测试指标
甲	3	7	20	40	20	10
乙	5	15	35	35	7	3

现将根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率．
（1）计算新工人乙生产三件产品A，给工厂带来盈利大于或等于100元的概率；
（2）记甲乙分别生产一件产品A给工厂带来的盈利和记为X，求随机变量X的概率分布和数学期望．

某市电视台在因特网上征集电视节目的现场参与观众，报名的共有12000人，分别来自4个城区，其中东城区2400人，西城区4600人，南城区3800人，北城区1200人，从中抽取60人参加现场节目，应当如何抽取？

设袋子中装有个红球，个黄球，个蓝球，且规定：取出一个红球得1分，
取出一个黄球2分，取出蓝球得3分。
（1）当时，从该袋子中任取（有放回，且每球取到的机会均等）2个球，记随机变量为取出此2球所得分数之和，.求分布列；
（2）从该袋子中任取（且每球取到的机会均等）1个球，记随机变量为取出此球所得分数.若，求

某高中有高级教师96人，中级教师144人，初级教师48人，为了进一步推进高中课程改革，邀请甲、乙、丙、丁四位专家到校指导。学校计划从所有教师中采用分层抽样办法选取6名教师分别与专家一对一交流，选出的6名教师再由专家随机抽取教师进行教学调研。
（1）求应从高级教师、中级教师、初级教师中分别抽取几人；
（2）若甲专家选取了两名教师，这两名教师分别是高级教师和中级教师的概率；
（3）若每位专家只抽一名教师，每位教师只与其中一位专家交流，求高级教师恰有一人被抽到的概率。

某校在一次趣味运动会的颁奖仪式上，高一、高二、高三各代表队人数分别为120人、120人、n人.为了活跃气氛，大会组委会在颁奖过程中穿插抽奖活动，并用分层抽样的方法从三个代表队中共抽取20人在前排就坐，其中高二代表队有6人.
（1）求n的值；
（2）把在前排就坐的高二代表队6人分别记为a，b，c，d，e，f，现随机从中抽取2人上台抽奖，.求a和b至少有一人上台抽奖的概率；

某班同学利用劳动节进行社会实践，对岁的人群随机抽取人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：

（1）补全频率分布直方图并求、、的值；
（2）从年龄段在的“低碳族”中采用分层抽样法抽取人参加户外低碳体验活动，其中每组各选多少人？

某工厂生产A、B、C三种不同型号的产品,产品数量之比为3:4:7,现用分层抽样的方法抽取
容量为的样本,样本中A型号产品有15件,那么样本容量为_______．

学校为了调查学生在课外读物方面的支出情况，抽取了一个容量为100的样本，
其频率分布直方图如图所示，则据此估计支出在[50,60）元的同学的概率为____________.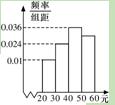

从甲、乙两班分别任意抽出10名学生进行英语口语测验，其测验成绩的方差分别为S₁²= 13.2，S₂²=26．26，则

A．甲班10名学生的成绩比乙班10名学生的成绩整齐

B．乙班10名学生的成绩比甲班10名学生的成绩整齐

C．甲、乙两班10名学生的成绩一样整齐

D．不能比较甲、乙两班10名学生成绩的整齐程度

某社团组织名志愿者利用周末和节假日参加社会公益活动,活动内容是：1、到各社区宣传慰问,倡导文明新风；2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下22的列联表所示：

	宣传慰问	义工	总计
20至40岁		16
大于40岁	15		23
总计		24	50

（1）填上表中所空缺的数值。
（2）分层抽样方法在做义工的志愿者中随机抽取6名,年龄在20至40岁与大于40岁的应该各抽取几名?
（3）根据（2）抽取的6名志愿者中任取2名，求选取的2人中分别来自上述年龄段各1人的概率。

将某班参加社会实践编号为：1，2，3，…，48的48名学生，采用系统抽样的方法抽取一个容量为6的样本，已知5号，21号，29号，37号，45号学生在样本中，则样本中还有一名学生的编号是 ．

下列四个命题：
①样本方差反映的是所有样本数据与样本平均值的偏离程度；
②某只股票经历了l0个跌停（每次跌停，即下跌l0%）后需再经过10个涨停（每次涨停，即上涨10%）
就可以回到原来的净值；
③某校高三一级部和二级部的人数分别是m、n，本次期末考试两级部；数学平均分分别是a、b，则这两
个级部的数学平均分为
④某中学采用系统抽样方法，从该校高一年级全体800名学生中抽50名学生做牙齿健康检查，现将800
名学生从001到800进行编号，已知从497--512这16个数中取得的学生编号是503，则初始在第1小组
00l～016中随机抽到的学生编号是007．
其中真命题的个数是（）

A．0个

B．1个

C．2个

D．3个