某高中有高级教师96人,中级教师144人,初级教师48人,为了进一步推进高中课程改革,邀请甲、乙、丙、丁四位专家到校指导。学校计划从所有教师中采用分层抽样办法选取6名教师分别与专家一对一交流,选出的6名教师再由专家随机抽取教师进行教学调研。
(1)求应从高级教师、中级教师、初级教师中分别抽取几人;
(2)若甲专家选取了两名教师,这两名教师分别是高级教师和中级教师的概率;
(3)若每位专家只抽一名教师,每位教师只与其中一位专家交流,求高级教师恰有一人被抽到的概率。
相关知识点
推荐套卷
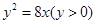 与直线
与直线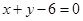 及
及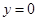 所围成图形的面积.
所围成图形的面积.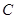 在直线
在直线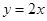 上,且经过原点及点
上,且经过原点及点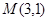 的圆
的圆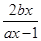 ,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.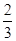 ,an+1=f(an),bn=
,an+1=f(an),bn= -1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
-1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;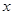 的不等式:
的不等式: 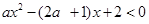
 粤公网安备 44130202000953号
粤公网安备 44130202000953号