已知向量a，b满足|a|=2|b|≠0，且关于x的函数f（x）=2x3－3| a |x2+6 a •b x+5在实数集R
上有极值，则向量a，b的夹角的取值范围是（）
A．（ ，π） |
B．（，π] |
| C．[，π] |
D．（0，） |
设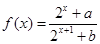
是定义在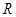
上的奇函数（
为实常数）．
（1）求
与
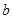的值；
（2）证明函数
的单调性并求函数的值域．
用
表示两数中的最小值，若函数
，则不等式
的解集是________________________．
已知函数
是R上的减函数则a的取值范围是（）
| A．（0，3） | B．（0，3] |
| C．（0，2） | D．（0，2] |
函数y=f（x）在[0，2]上单调递增，且函数f（x+2）是偶函数，则下列结论成立的是（）
A．f（1）＜f（ ）＜f（ ） |
| B．f（）＜f（1）＜f（） |
| C．f（）＜f（）＜f（1） |
| D．f（）＜f（1）＜f（） |
以A表示值域为R的函数组成的集合，B表示具有如下性质的函数
组成的集合：对于函数，存在一个正数M，使得函数的值域包含于区间
．例如，当
．现有如下命题：
①设函数
的定义域为D，则“
”的充要条件是“
”；
②函数
的充要条件是有最大值和最小值；
③若函数，
的定义域相同，且
④若函数
有最大值，则．
其中的真命题为（）
| A．①③ | B．②③ | C．①②④ | D．①③④ |
是R上的增函数，点
、
是其图象上的两点，那么不等式
＜1的解集的补集是（）
时，求函数的最大值和最小值；
的取值范围，使得函数
在区间
上是单调函数．
为定义在
上的偶函数，且在
内是增函数，又
，则不等式
的解集为（）
在区间
上是增函数，则实数a的取值范围是 ．
在
内有最小值，则实数
的取值范围是（）
的单调减区间是 ．
在区间
上恒成立，则实数m的取值范围是 .
的单调增区间是（）
粤公网安备 44130202000953号