设点P是曲线y=2x2上的一个动点,曲线y=2x2在点P处的切线为l,过点P且与直线l垂直的直线与曲线y=2x2的另一交点为Q,则PQ的最小值为_____________
已知函数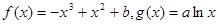 .
.
(Ⅰ)若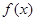 在
在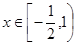 上的最大值为
上的最大值为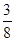 ,求实数
,求实数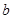 的值;
的值;
(Ⅱ)若对任意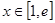 ,都有
,都有 恒成立,求实数
恒成立,求实数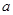 的取值范围;
的取值范围;
(Ⅲ)在(Ⅰ)的条件下,设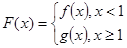 ,对任意给定的正实数
,对任意给定的正实数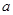 ,曲线
,曲线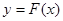 上是否存在两点
上是否存在两点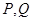 ,使得
,使得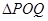 是以
是以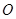 (
(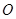 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在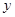 轴上?请说明理由.
轴上?请说明理由.
设函数 ,
, 是定义域为R上的奇函数.
是定义域为R上的奇函数.
(1)求 的值,并证明当
的值,并证明当 时,函数
时,函数 是R上的增函数;
是R上的增函数;
(2)已知 ,函数
,函数 ,
, ,求
,求 的值域;
的值域;
(3)若 ,试问是否存在正整数
,试问是否存在正整数 ,使得
,使得 对
对 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数 ;若不存在,请说明理由.
;若不存在,请说明理由.
已知函数 ,其中常数
,其中常数 .
.
(1)求 的单调区间;
的单调区间;
(2)如果函数 在公共定义域D上,满足
在公共定义域D上,满足 ,那么就称
,那么就称 为
为 与
与 的“和谐函数”.设
的“和谐函数”.设 ,求证:当
,求证:当 时,在区间
时,在区间 上,函数
上,函数 与
与 的“和谐函数”有无穷多个.
的“和谐函数”有无穷多个.
已知f(x)= (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(1)求实数a的值组成的集合A;
(2)设关于x的方程f(x)= 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
(本小题14分)已知函数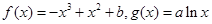 .
.
(1)若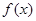 在
在 上的最大值为
上的最大值为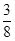 ,求实数
,求实数 的值;
的值;
(2)若对任意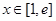 ,都有
,都有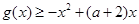 恒成立,求实数
恒成立,求实数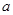 的取值范围;
的取值范围;
(3)在(1)的条件下,设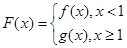 ,对任意给定的正实数
,对任意给定的正实数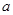 ,曲线
,曲线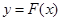 上是否存在两点
上是否存在两点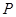 、
、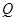 ,使得
,使得 是以
是以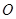 (
(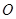 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在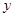 轴上?请说明理由。
轴上?请说明理由。
已知△ABC的三个内角A、B、C所对的边分别为a、b、c,向量

(Ⅰ)求角A的大小;
(Ⅱ)若 ,试判断b·c取得最大值时△ABC形状.
,试判断b·c取得最大值时△ABC形状.
(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
已知 ,且
,且 ,
, ,数列
,数列 、
、 满足
满足 ,
, ,
, ,
, .
.
(1) 求证数列 是等比数列;
是等比数列;
(2) (理科)求数列 的通项公式
的通项公式 ;
;
(3) (理科)若 满足
满足 ,
, ,
, ,试用数学归纳法证明:
,试用数学归纳法证明: .
.