如图,已知椭圆C: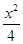 +y2=1,A、B是四条直线x=±2,y=±1所围成的两个顶点.
+y2=1,A、B是四条直线x=±2,y=±1所围成的两个顶点.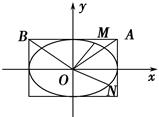
(1)设P是椭圆C上任意一点,若 =m
=m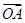 +n
+n ,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
(2)若M、N是椭圆C上两上动点,且直线OM、ON的斜率之积等于直线OA、OB的斜率之积,试探求△OMN的面积是否为定值,说明理由.
双曲线 =1(a>0,b>0)的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1,2)在“上”区域内,则双曲线离心率e的取值范围是________.
=1(a>0,b>0)的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1,2)在“上”区域内,则双曲线离心率e的取值范围是________.
如图是见证魔术师“论证”64=65飞神奇.对这个乍看起来颇为神秘的现象,我们运用数学知识不难发现其中的谬误.另外,我们可以更换图中的数据,就能构造出许多更加直观与“令人信服”的“论证”.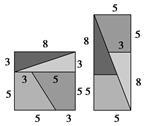
请你用数列知识归纳:(1)这些图中的数所构成的数列:________;(2)写出与这个魔术关联的一个数列递推关系式:________.
设 ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 作倾斜角为
作倾斜角为 的直线交椭圆
的直线交椭圆 于
于 ,
, 两点,
两点,  到直线
到直线 的距离为
的距离为 ,连结椭圆
,连结椭圆 的四个顶点得到的菱形面积为
的四个顶点得到的菱形面积为 .
.
(1)求椭圆 的方程;
的方程;
(2)过椭圆 的左顶点
的左顶点 作直线
作直线 交椭圆
交椭圆 于另一点
于另一点 , 若点
, 若点 是线段
是线段 垂直平分线上的一点,且满足
垂直平分线上的一点,且满足 ,求实数
,求实数 的值.
的值.
如图,椭圆 的离心率为
的离心率为 ,
, 轴被曲线
轴被曲线 截得的线段长等于
截得的线段长等于 的短轴长。
的短轴长。 与
与 轴的交点为
轴的交点为 ,过坐标原点
,过坐标原点 的直线
的直线 与
与 相交于点
相交于点 ,直线
,直线 分别与
分别与 相交于点
相交于点 。
。
(1)求 、
、 的方程;
的方程;
(2)求证: 。
。
(3)记 的面积分别为
的面积分别为 ,若
,若 ,求
,求 的取值范围。
的取值范围。
已知椭圆 的离心率与双曲线
的离心率与双曲线 的离心率互为倒数,直线
的离心率互为倒数,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(1)求椭圆 的方程;
的方程;
(2)设椭圆 的左焦点为
的左焦点为 ,右焦点为
,右焦点为 ,直线
,直线 过点
过点 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线 垂直
垂直 于点
于点 ,线段
,线段 垂直平分线交
垂直平分线交 于点
于点 ,求点
,求点 的轨迹
的轨迹 的方程;
的方程;
(3)设第(2)问中的 与
与 轴交于点
轴交于点 ,不同的两点
,不同的两点 在
在 上,且满足
上,且满足 ,求
,求 的取值范围.
的取值范围.
已知离心率为 的椭圆
的椭圆 (
( )过点
)过点
(1)求椭圆 的方程;
的方程;
(2)过点 作斜率为
作斜率为 直线
直线 与椭圆相交于
与椭圆相交于 两点,求
两点,求 的长.
的长.
已知直线l:y=x+ ,圆O:x2+y2=5,椭圆E:
,圆O:x2+y2=5,椭圆E: =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,直线l被圆O截得的弦长与椭圆的短轴长相等.
,直线l被圆O截得的弦长与椭圆的短轴长相等.
(1)求椭圆E的方程;
(2)过圆O上任意一点P作椭圆E的两条切线,若切线都存在斜率,求证:两条切线的斜率之积为定值.
如图,在平面直角坐标系xOy中,椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以坐标原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
,以坐标原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
(1)求椭圆C的方程;
(2)已知点P(0,1),Q(0,2),设M,N是椭圆C上关于y轴对称的不同两点,直线PM与QN相交于点T.求证:点T在椭圆C上.
已知数列{an}的前n项和是Sn,且Sn+ an=1.
an=1.
(1)求数列{an}的通项公式;
(2)记bn=log3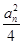 ,数列
,数列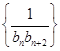 的前n项和为Tn,证明:Tn<
的前n项和为Tn,证明:Tn< .
.
已知数列{an}是公差不为0的等差数列,{bn}是等比数列,其中a1=3,b1=1,a2=b2,3a5=b3,若存在常数u,v对任意正整数n都有an=3logubn+v,则u+v=________.
设F1,F2分别是椭圆E:x2+ =1(0<b<1)的左、右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
=1(0<b<1)的左、右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
(1)求|AB|;
(2)若直线l的斜率为1,求b的值.
已知椭圆中心在坐标原点,焦点在x轴上,离心率为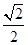 ,它的一个顶点为抛物线x2=4y的焦点.
,它的一个顶点为抛物线x2=4y的焦点.
(1)求椭圆方程;
(2)若直线y=x-1与抛物线相切于点A,求以A为圆心且与抛物线的准线相切的圆的方程;
(3)若斜率为1的直线交椭圆于M、N两点,求△OMN面积的最大值(O为坐标原点).
设定义在R上的函数f(x)是最小正周期为2π的偶函数;f′(x)是f(x)的导函数,当x∈[0,π]时,0<f(x)<1;当x∈(0,π)且x≠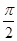 时,
时,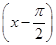 f′(x)>0.则函数y=f(x)-sin x在[-2π,2π]上的零点个数为________.
f′(x)>0.则函数y=f(x)-sin x在[-2π,2π]上的零点个数为________.
设点P在曲线y=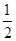 ex上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为( ).
ex上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为( ).
| A.1-ln 2 | B.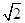 (1-ln 2) (1-ln 2) |
C.1+ln 2 | D.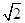 (1+ln 2) (1+ln 2) |