2014年高考数学(理)二轮复习专题能力测评6练习卷
若k,-1,b三个数成等差数列,则直线y=kx+b必经过定点( ).
| A.(1,-2) | B.(1,2) | C.(-1,2) | D.(-1,-2) |
在平面直角坐标系xOy中,直线3x+4y-5=0与圆x2+y2=4相交于A、B两点,则弦AB的长等于( ).
A.3 |
B.2 |
C. |
D.1 |
若双曲线 =1的离心率为
=1的离心率为 ,则其渐近线方程为( ).
,则其渐近线方程为( ).
| A.y=±2x | B.y=± x x |
C.y=± x x |
D.y=± x x |
若圆心在x轴上、半径为 的圆O位于y轴左侧,且与直线x+2y=0相切,则圆O的方程是( ).
的圆O位于y轴左侧,且与直线x+2y=0相切,则圆O的方程是( ).
A.(x- )2+y2=5 )2+y2=5 |
B.(x+ )2+y2=5 )2+y2=5 |
| C.(x-5)2+y2=5 |
| D.(x+5)2+y2=5 |
已知点M( ,0),椭圆
,0),椭圆 +y2=1与直线y=k(x+
+y2=1与直线y=k(x+ )交于点A、B,则△ABM的周长为( ).
)交于点A、B,则△ABM的周长为( ).
| A.4 | B.8 | C.12 | D.16 |
已知0<θ< ,则双曲线C1:
,则双曲线C1: =1与C2:
=1与C2: =1的( ).
=1的( ).
| A.实轴长相等 | B.虚轴长相等 | C.焦距相等 | D.离心率相等 |
直线l过抛物线C:x2=4y的焦点且与y轴垂直,则l与C所围成的图形的面积等于( ).
A. |
B.2 | C. |
D. |
双曲线 =1(m>0,n>0)的离心率为2,有一个焦点与抛物线y2=4mx的焦点重合,则n的值为( ).
=1(m>0,n>0)的离心率为2,有一个焦点与抛物线y2=4mx的焦点重合,则n的值为( ).
| A.1 | B.4 | C.8 | D.12 |
设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为( ).
| A.y2=4x或y2=8x | B.y2=2x或y2=8x |
| C.y2=4x或y2=16x | D.y2=2x或y2=16x |
l1,l2是分别经过A(1,1),B(0,-1)两点的两条平行直线,当l1,l2间的距离最大时,直线l1的方程是________.
P是椭圆 =1上的任意一点,F1、F2是它的两个焦点,O为坐标原点,有一动点Q满足
=1上的任意一点,F1、F2是它的两个焦点,O为坐标原点,有一动点Q满足 =
= +
+ ,则动点Q的轨迹方程是________.
,则动点Q的轨迹方程是________.
已知圆C的方程为:x2+y2-2mx-2y+4m-4=0.(m∈R).
(1)试求m的值,使圆C的面积最小;
(2)求与满足(1)中条件的圆C相切,且过点(1,-2)的直线方程.
如图所示,已知椭圆 =1(a>b>0)的右焦点为F2(1,0),点A
=1(a>b>0)的右焦点为F2(1,0),点A 在椭圆上.
在椭圆上.
(1)求椭圆方程;
(2)点M(x0,y0)在圆x2+y2=b2上,点M在第一象限,过点M作圆x2+y2=b2的切线交椭圆于P、Q两点,问| |+|
|+| |+|
|+| |是否为定值?如果是,求出该定值;如果不是,说明理由.
|是否为定值?如果是,求出该定值;如果不是,说明理由.
在平面直角坐标系xOy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为 .
.
(1)求抛物线C的方程.
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M的坐标;若不存在,说明理由.
 y=0的距离是( ).
y=0的距离是( ). -y2=1的顶点到其渐近线的距离等于________.
-y2=1的顶点到其渐近线的距离等于________.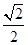 ,它的一个顶点为抛物线x2=4y的焦点.
,它的一个顶点为抛物线x2=4y的焦点. 粤公网安备 44130202000953号
粤公网安备 44130202000953号