已知在半径为4的球面上有A、 B、 C、 D四个点,且AB=CD=4,则四面体ABCD体积最大值为( )
A.  B.
B. C. 4
C. 4 D.
D.
已知三棱柱ABC—A1B1C1的侧棱与底面边长都相等,A1在底面ABC内的射影为DABC的中心,则AB1与底面ABC所成角的正弦值为( )
A. |
B.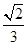 |
C. |
D. |
有棱长为6的正四面体SABC,A¢,B¢,C¢分别在棱SA,SB,SC上,且SA¢=2,SB¢=3,SC¢=4,则截面A¢B¢C¢将此正四面体分成的两部分体积之比为( )
A. |
B. |
C. |
D.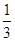 |
某几何体的一条棱长为 ,在该几何体的正视图中,这条棱的投影是长为
,在该几何体的正视图中,这条棱的投影是长为 的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为( )
的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为( )
A.2 |
B.2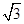 |
C.4 | D.2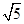 |
设DABC的一个顶点是A(3,-1), ÐB, ÐC的平分线所在直线方程分别为x="0,y=x" , 则直线BC的方程为( )
| A. y=2x+5 | B. y=2x+2 |
| C. y=3x+5 | D. y=-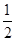 x+ x+ |
已知a,b满足a+2b=1,则直线ax+3y+b=0必过定点( )
A.(- , , ) ) |
B. ( , , ) ) |
C. ( , - , - ) ) |
D. ( , - , - ) ) |
下列命题正确的是( )
| A.若两条直线和同一个平面所成的角相等, 则这两条直线平行; |
| B.若一个平面内有三点到另一个平面的距离相等,则这两个平面平行; |
| C.若一条直线和两个相交平面都平行, 则这条直线与这两个平面的交线平行; |
| D.若两个平面都垂直于第三个平面, 则这两个平面平行. |
知椭圆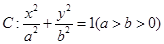 的离心率为
的离心率为 ,定点
,定点 ,椭圆短轴的端点是
,椭圆短轴的端点是 ,且
,且 .
.
(1)求椭圆 的方程;
的方程;
(2)设过点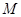 且斜率不为0的直线交椭圆
且斜率不为0的直线交椭圆 于
于 两点.试问
两点.试问 轴上是否存在异于
轴上是否存在异于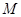 的定点
的定点 ,使
,使 平分
平分 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
一个袋子里装有7个球,其中有红球4个, 编号分别为1,2,3,4;白球3个,编号分别为1,2,3.从袋子中任取4个球(假设取到任何一个球的可能性相同).
(Ⅰ)求取出的4个球中, 含有编号为3的球的概率;
(Ⅱ)在取出的4个球中, 红球编号的最大值设为X,求随机变量X的分布列和数学期望.