初中数学四种命题及其关系试题

一电工沿着如图所示的梯子NL往上爬，当他爬到中点M处时，由于地面太滑，梯
子沿墙面与地面滑下，设点M的坐标为（x，y）（x>0）,则y与x之间的函数关系用图象表
示大致是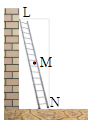   
     

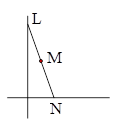
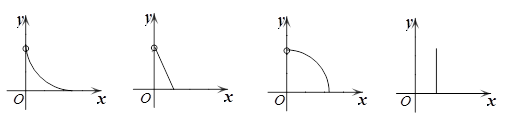
A．                B．             C．              D．

如图，在直角梯形ABCD中，∠D=∠BCD=90°，∠B=60°， AB=6，AD=9，
点E是CD上的一个动点(E不与D重合)，过点E作EF∥AC，交AD于点F(当E运
动到C时，EF与AC重合巫台)．把△DEF沿EF对折，点D的对应点是点G，设DE=x，
△GEF与梯形ABCD重叠部分的面积为y。
(1) 求CD的长及∠1的度数；
(2) 若点G恰好在BC上，求此时x的值；
(3) 求y与x之间的函数关系式。并求x为何值时，y的值最大?最大值是多少?

下列图象中，能反映函数y随x增大而减小的是

如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数（m≠0）的图象相交于A、B两点．求：
（1）根据图象写出A、B两点的坐标并分别求出反比例函数和一次函数的解析式；
（2）根据图象写出：当x为何值时，一次函数值大于反比例函数值．

如图，直线(＞0)与双曲线在第一象限内的交点为R，与轴
的交点为P，与轴的交点为Q；作RM⊥轴于点M，若△OPQ与△PRM的面积是9∶1，则
  ▲ ．

（11·贵港）若记y＝f(x)＝，其中f(1)表示当x＝1时y的值，即f(1)＝
＝；f()表示当x＝时y的值，即f()＝＝；…；则f(1)＋f(2)＋f()＋f(3)
＋f()＋…＋f(2011)＋f()＝_  ▲  ．

如图，在平面直角坐标系中有一矩形ABCD黑色区域，其中，  ，
C（2,1），D（2,2），有一动态扫描线为双曲线（x＞0），当扫描线遇到黑色区域时，区
域便由黑变白，则能够使黑色区域变白的k的取值范围是

A．4≤k≤6	B．2≤k≤12
C．6＜k＜12	D．2＜k＜12

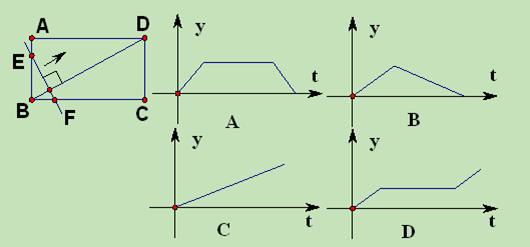
如图所示，在矩形ABCD中，垂直于对角线BD的直线 ，从点B开始沿着线段BD匀速平移到D．设直线 被矩形所截线段EF的长度为y，运动时间为t，则y关于t的函数的大致图象是（   ）

下列函数中，当x＞0时，y值随x值增大而减小的是（　　）

A．y=x^2	B．y=x﹣1
C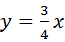．	D．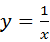

如下图，在平面直角坐标系中，对△ABC进行循环
往复的轴对称或中心对称变换，若原来点A坐标是（a，b），则经过第2011次变换后所得
的A点坐标是________．

二次函数的图像如图，则反比例函数y=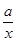－与一次函数y=bx+c的图像在同一坐标系内的图像大致是

（11·佛山）下列函数的图像在每一个象限内，y值随x值的增大而增大的是（      ）

下列四个图象表示的函数中，当x＜0时，函数值y随自变量x的增大而减小的是（   ）

如图，边长都为1的正方形和正三角形，其一边在同一水平线上，三角形沿该水平线自左向右匀速穿过正方形。设穿过的时间为t，正方形与三角形重合部分的面积为S，那么S关于t的函数大致图象应为（  ）

 

如图2，火车匀速通过隧道（隧道长等于火车长）时，火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图像描述大致是（    ）