2011年初中毕业升学考试(广东广州卷)数学解析版
在平面直角坐标系中,下面的点在第一象限的是
| A. | (1,2) | B. | (-2,3) | C. | (0,0) | D. | (-3,-2) |
因式分解x2y-4y的正确结果是
| A.y(x+2)(x-2) | B.y(x+4)(x-4) |
| C.y(x2-4) | D.y(x-2)2 |
如图1,直线EO⊥CD,垂足为点O,AB平分∠EOD,
则∠BOD的度数为
| A.120° | B.130° | C.135° | D.140° |

如图是从一幅扑克牌中取出的两组牌,分别是黑桃1,2,3,4红桃1,2,3,4,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,那么摸出的两张牌面数字之和等于7的概率是
A. |
B. |
C. |
D. |

如图,在平面直角坐标系中,直线
与矩形
的边
、
分别交于点
、
,已知
,
,则
的面积是

(A)6 (B)3 (C)12 (D)
2011年5月22日—29日在美丽的青岛市举行了苏
迪曼杯羽毛球混合团体锦标赛.在比赛中,某次羽毛球的运动路线可以看作是抛物线 的一部分(如图5),其中出球点B离地面O点的距离是1m,球落地
的一部分(如图5),其中出球点B离地面O点的距离是1m,球落地
点A到O点的距离是4m,那么这条抛物线的解析式是

如图6,点B、C、E在同一条直线上,△ABC与△
CDE都是等边三角形,则下列结论不一定成立的是
(A)△ACE≌△BCD (B)△BGC≌△AFC
(C)△DCG≌△ECF (D)△ADB≌△CEA
图9是由两个长方体组合而成的一个立体图形的三
视图,根据图中所标尺寸(单位:mm),计算出这个立体图形的表面积是________mm2.
如下图,在平面直角坐标系中,对△ABC进行循环
往复的轴对称或中心对称变换,若原来点A坐标是(a,b),则经过第2011次变换后所得
的A点坐标是________.
已知B(2,n)是正比例函数y=2x图象上的点.
(1)求点B的坐标;
(2)若某个反比例函数图象经过点B,求这个反比例函数的解析式.
在今年法国网球公开赛中,我国选手李娜在决赛中
成功击败对手夺冠,称为获得法国网球公开赛冠军的亚洲第一人.某班体育委员就本班同学
对该届法国网球公开赛的了解程度进行全面调查统计,收集数据后绘制了两幅不完整的统计
图,如图(1)和图(2).根据图中的信息,解答下列问题:
(1)该班共有________名学生;
(2)在图(1)中,“很了解”所对应的圆心角的度数为_________;
(3)把图(2)中的条形图形补充完整.
如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察
由于受金融危机的影响,某店经销的甲型号手机今年的售价比去年每台降价500元.如果卖出相同数量的手机,那么去年销售额为8万元,今年销售额只有6万元.
(1)今年甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划购进乙型号手机销售,已知甲型号手机每台进价为1000元,乙型号手机每台进价为800元,预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)若乙型号手机的售价为1400元,为了促销,公司决定每售出一台乙型号手机,返还顾客现金a元,而甲型号手机仍按今年的售价销售,要使(2)中所有方案获利相同,a应取何值?
如图,AB是⊙O的直径,CD是⊙O的切线,切点为C.延长AB交CD于点E.连接AC,作∠DAC=∠ACD,作AF⊥ED于点F,交⊙O于点G.
(1)求证:AD是⊙O的切线;
(2)如 果⊙O的半径是6cm,EC=8cm,求GF的长.
果⊙O的半径是6cm,EC=8cm,求GF的长.
某车间5名工人日加工零件数分别为6,10,4,5,4,则这组数据的中位数是( )
| A.4 | B.5 |
| C.6 | D.10 |
将点A(2,1)向左平移2个单位长度得到点A′,则点A′的坐标是( )
| A.(0,1) | B.(2,﹣1) |
| C.(4,1) | D.(2,3) |
若a<c<0<b,则abc与0的大小关系是( )
| A.abc<0 | B.abc=0 |
| C.abc>0 | D.无法确定 |
下面的计算正确的是( )
| A.3x2•4x2=12x2 | B.x3•x5=x15 |
| C.x4÷x=x3 | D.(x5)2=x7 |
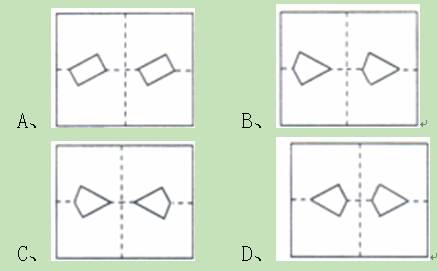
如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )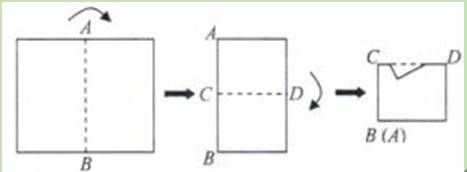
当实数x的取值使得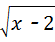 有意义时,函数y=4x+1中y的取值范围是( )
有意义时,函数y=4x+1中y的取值范围是( )
| A.y≥﹣7 | B.y≥9 |
| C.y>9 | D.y≤9 |
如图,AB切⊙O于点B,OA=2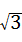 ,AB=3,弦BC∥OA,则劣弧BC的弧长为( )
,AB=3,弦BC∥OA,则劣弧BC的弧长为( )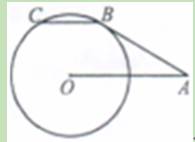
A.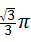 |
B.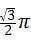 |
| C.π | D.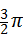 |
如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm,OA′=20cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是_________.
已知三条不同的直线a、b、c在同一平面内,下列四条命题:
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中真命题的是__________.(填写所有真命题的序号)
如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.求证:△ACE≌△ACF.
5个棱长为1的正方体组成如图的几何体.
(1)该几何体的体积是______(立方单位),表面积是_________(平方单位)
(2)画出该几何体的主视图和左视图.
某商店5月1日举行促销优惠活动,当天到该商店购买商品有两种方案,方案一:用168元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的8折优惠;方案二:若不购买会员卡,则购买商店内任何商品,一律按商品价格的9.5折优惠.已知小敏5月1日前不是该商店的会员.
(1)若小敏不购买会员卡,所购买商品的价格为120元时,实际应支付多少元?
(2)请帮小敏算一算,所购买商品的价格在什么范围时,采用方案一更合算?
某中学九年级(3)班50名学生参加平均每周上网时间的调查,由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
(1)求a的值;
(2)用列举法求以下事件的概率:从上网时间在6~10小时的5名学生中随机选取2人,其中至少有1人的上网时间在8~10小时.
已知Rt△ABC的斜边AB在平面直角坐标系的x轴上,点C(1,3)在反比例函数y= 的图象上,且sin∠BAC=
的图象上,且sin∠BAC= .
.
(1)求k的值和边AC的长;
(2)求点B的坐标.
已知关于x的二次函数 的图象经过点 ,且与x轴交于不同的两点 、 ,点 的坐标是 .
(1)求
的值;
(2)求
的取值范围;
(3)该二次函数的图象与直线 交于 , 两点,设1, 的面积为 ,当 时,求证: 为常数,并求出该常数.






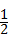 ,
,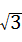 中为无理数的是( )
中为无理数的是( )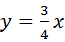
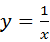
 的解是____________.
的解是____________. ,则12⊗(﹣1)=________
,则12⊗(﹣1)=________ .
. OM;
OM;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号