初中数学一次函数的最值试题

某气球内充满一定质量的气体，当温度不变时，气球内气体的气压p（kPa）是气体体积V（m³）的反比例函数，其图象如图所示．

（1）写出这一函数的表达式．
（2）当气体体积为1 m³时，气压是多少？
（3）当气球内的气压大于140 kPa时，气球将爆炸，为了安全考虑，气体的体积应不小于多少？

如图1是甲、乙两个圆柱形水槽的轴截面示意图，乙槽中有一圆柱形块放其中（圆柱形铁块的下底面完全落在水槽底面上）现将甲槽中的水匀速注入乙槽，甲、乙两个水槽中水的深度y（厘米）与注水时间x（分钟）之间的关系如图2所示．根据图象提供的信息，解答下列问题：

（1）图2中折线ABC表示     槽中的深度与注水时间之间的关系，线段DE表示    槽中的深度与注水时间之间的关系（以上两空选填“甲”、或“乙”），点B的纵坐标表示的实际意义是                        
（2）注水多长时间时，甲、乙两个水槽中的水的深度相同？
（3）若乙槽底面积为36平方厘米（壁厚不计），求乙槽中铁块的体积；
（4）若乙槽中铁块的体积为112立方厘米（壁厚不计），求甲槽底面积．

已知一次函数y=kx+b图象过点（0，2），且与两坐标轴围成的三角形面积为2，求此一次函数的解析式．

某学校要印制一批《学生手册》，甲印刷厂提出：每本收1元印刷费，另收500元制版费；乙印刷厂提出：每本收2元印刷费，不收制版费．
（1）分别写出甲、乙两厂的收费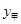 （元）、（元）与印制数量x（本）之间的关系式；
（2）问：该学校选择哪间印刷厂印制《学生手册》比较合算？请说明理由．

如图，直线与x轴、y轴分别交于A、B两点，把△AOB绕点A旋转90°后得到△AO’B’，则点B’的坐标是                 ．

直线l对应的一次函数关系式为y＝x－2，若把直线向上平移3个单位，则所得函数的解析式为                ．

在平面直角坐标系中，已知一次函数y＝2x＋1的图像经过P₁（x₁,y₁）,P₂（x₂,y₂）两点，若x₁＜x₂，则y₁________y₂．（填“>”，“<”或“＝”）

一名考生步行前往考场， 10分钟走了总路程的1/4，估计步行不能准时到达，于是他改乘出租车赶往考场，他的行程与时间关系如图所示（假定总路程为1），则他到达考场所花的时间比一直步行提前了（       ）

A．20分钟

B．22分钟

C．24分钟

D．26分钟

如图，正比例函数和一次函数的图象相交于A（m,3），则不等式的解集为（   ）

A．

B．

C．

D．

已知一次函数y＝kx－1，若y随x的增大而增大，则它的图象经过（      ）

A．第一、二、三象限	B．第一、二、四象限
C．第一、三、四象限	D．第二、三、四象限

若点A（2，4）在函数y＝kx－2的图象上，则下列各点在此函数图象上的是（    ）

A．（1，1）

B．（－1，1）

C．（－2，－2）

D．（2，－2）

如图，直线的函数关系式为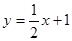，且与x轴交于点D，直线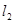经过定点A（4，0），B（-1，5），直线与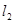相交于点C，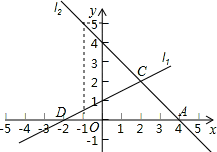

（1）求直线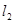的解析式；
（2）求△ADC的面积；
（3）在直线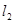上存在一点F（不与C重合），使得△ADF和△ADC的面积相等，请求出F点的坐标；
（4）在x轴上是否存在一点E，使得△BCE的周长最短，若存在请求出E点的坐标，若不存在，请说明理由．

已知甲、乙两地相距300km，小轿车从甲地出发驶往乙地，同时货车从相距乙地60km的入口A处驶往甲地（两车均在甲、乙两地之间的公路上匀速行驶），如图是它们离甲地的路程y（km）与货车行驶时间x（h）之间的函数的部分图像．

（1）求货车离甲地的路程y（km）与它行驶的时间x（h）的函数表达式；
（2）哪一辆车先到达目的地（小轿车达到乙地；货车到达甲地）？说明理由．

小明从兴化通过申通快递公司给在南京的朋友寄一盒苹果，快递时，他了解到申通快递公司除了收取每次6元的包装费外，苹果不超过2kg时收费22元，若超过2kg，则超过的部分按每千克10元收取费用，该公司从兴化到南京快递苹果的费用为y（元），小明所寄的苹果为x（kg）（x＞2）
（1）求y与x的函数关系式；
（2）已知小明给朋友寄了2．5kg的苹果，请你求出这次快递的费用．

用图像法求二元一次方程组的解．