将二次函数 的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是 ▲
的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是 ▲
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①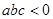 ②当
②当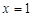 时,函数有最大值。③当
时,函数有最大值。③当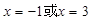 时,函数y的值都等于0. ④
时,函数y的值都等于0. ④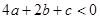 其中正确结论的个数是( )
其中正确结论的个数是( )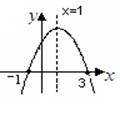
| A.1 | B.2 | C.3 | D.4 |
如图①,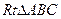 中,
中,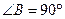
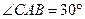 ,
,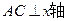 .它的顶点
.它的顶点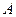 的坐标为
的坐标为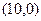 ,顶点
,顶点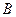 的坐标为
的坐标为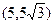 ,点
,点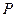 从点
从点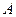 出发,沿
出发,沿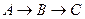 的方向匀速运动,同时点
的方向匀速运动,同时点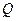 从点
从点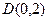 出发,沿
出发,沿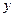 轴正方向以相同速度运动,当点
轴正方向以相同速度运动,当点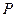 到达点
到达点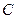 时,两点同时停止运动,设运动的时间为
时,两点同时停止运动,设运动的时间为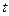 秒.
秒.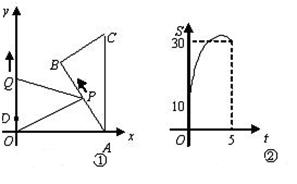
(1)求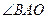 的度数.(直接写出结果)
的度数.(直接写出结果)
(2)当点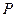 在
在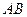 上运动时,
上运动时,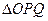 的面积
的面积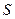 与时间
与时间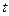 (秒)之间的函数图象为抛物线的一部分(如图②),求点
(秒)之间的函数图象为抛物线的一部分(如图②),求点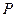 的运动速度.
的运动速度.
(3)求题(2)中面积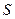 与时间
与时间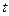 之间的函数关系式,及面积
之间的函数关系式,及面积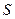 取最大值时点
取最大值时点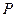 的坐标.
的坐标.
(4)如果点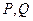 保持题(2)中的速度不变,当t取何值时,PO=PQ,请说明理由.
保持题(2)中的速度不变,当t取何值时,PO=PQ,请说明理由.
心理学家经过调查发现,某班级的学生对概念的接受能力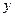 与提出概念所用的时间
与提出概念所用的时间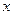 (单位:分)之间满足函数关系:
(单位:分)之间满足函数关系: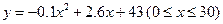 .其中,
.其中,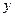 值越大,表示接受能力越强.
值越大,表示接受能力越强.
(1)第10分钟时,学生的接受能力是多少?
(2)第几分时,学生的接受能力最强?
(3)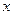 在什么范围内,学生的接受能力逐步增强?
在什么范围内,学生的接受能力逐步增强?
已知二次函数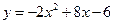 .
.
(1)求二次函数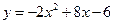 的图象与两个坐标轴的交点坐标;
的图象与两个坐标轴的交点坐标;
(2)在坐标平面上,横坐标与纵坐标都是整数的点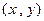 称为整点. 直接写出二次函数
称为整点. 直接写出二次函数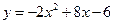 的图象与
的图象与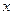 轴所围成的封闭图形内部及边界上的整点的个数.
轴所围成的封闭图形内部及边界上的整点的个数.
已知二次函数 .
.
(1)求此二次函数图像与x轴交点A、B(A在B的左边)的坐标;
(2)若此二次函数图像与y轴交于点C、且△AOC∽△COB(字母依次对应).
①求a的值;
②求此时函数图像上关于原点中心对称的两个点的坐标.
已知二次函数 的图像经过点
的图像经过点 与
与 .
.
(1)求此函数的解析式;
(2)用配方法求此函数图像的顶点坐标.
已知函数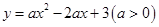 图像上点(2,n)与(3,m),则 n ▼ m. (填“>,<,或无法确定”)
图像上点(2,n)与(3,m),则 n ▼ m. (填“>,<,或无法确定”)
二次函数 的图像如图所示,则下列关系式中错误的是( ▼ )
的图像如图所示,则下列关系式中错误的是( ▼ )
A. |
B. |
C. |
D. |
如图,已知抛物线与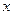 轴交于点
轴交于点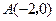 ,
,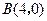 ,与y轴交于点
,与y轴交于点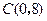 .
.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交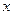 轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
随着本区近几年城市建设的快速发展,对花木的需求量逐年提高。某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润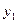 与投资量
与投资量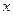 成正比例关系,如图(1)所示;种植花卉的利润
成正比例关系,如图(1)所示;种植花卉的利润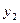 与投资量
与投资量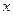 成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)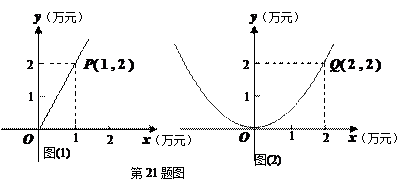
已知二次函数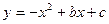 的图像经过A(-1,-6)、B(2,-3),求这个函数的解析式及这个函数图像的顶点坐标
的图像经过A(-1,-6)、B(2,-3),求这个函数的解析式及这个函数图像的顶点坐标