如图,在平面直角坐标系xOy中, 正方形OABC的边长为2cm, 点A、C分别在y轴的负半轴和x轴的正半轴上, 抛物线y=a +bx+c经过点A、B,最低点为M,且
+bx+c经过点A、B,最低点为M,且 =
=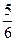

(1)求此抛物线的解析式.,并说明这条抛物线是由抛物线y=a 怎样平移得到的。
怎样平移得到的。
(2)如果点P由点A开始沿着射线AB以2cm/s的速度移动, 同时点Q由点B开始沿BC边以1cm/s的速度向点C移动,当其中一点到达终点时运动结束.
①在运动过程中,P、Q两点间的距离是否存在最小值,如果存在,请求出它的最小值。
②当PQ取得最小值时, 在抛物线上是否存在点R, 使得以P、B、Q、R为顶点的四边形是梯形? 如果存在, 求出R点的坐标, 如果不存在, 请说明理由.
二次函数 的图象如图所示,
的图象如图所示, 点
点 位于坐标原点, 点
位于坐标原点, 点 ,
, ,
, ,…,
,…,  在y轴的正半轴上,点
在y轴的正半轴上,点 ,
, ,
, ,…,
,…,  在二次函数
在二次函数 位于第一象限的图象上,若△
位于第一象限的图象上,若△ ,△
,△ ,△
,△ ,…,
,…, 都为等边三角形,则
都为等边三角形,则 的边长= .
的边长= .
已知:如图,抛物线 与
与 轴交于点
轴交于点 、点
、点 ,与直线
,与直线 相交于点
相交于点 、点
、点 ,直线
,直线 与
与 轴交于点
轴交于点 。
。
(1)求直线 的解析式;
的解析式;
(2)求 的面积;
的面积;
(3)若点 在线段
在线段 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从 向
向 运动(不与
运动(不与 重合),同时,点
重合),同时,点 在射线
在射线 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从 向
向 运动.设运动时间为
运动.设运动时间为 秒,请写出
秒,请写出 的面积
的面积 与
与 的函数关系式,并求出点
的函数关系式,并求出点 运动多少时间时,
运动多少时间时, 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?
如图,已知二次函数 的图象经过A(2,0)、B(0,-6)两点.
的图象经过A(2,0)、B(0,-6)两点.
(1)求这个二次函数的表达式;
(2)设该二次函数的对称轴与 轴交于点C,连结BA、BC,求△ABC的面积
轴交于点C,连结BA、BC,求△ABC的面积
已知点A(1,1)在二次函数y=x2-2ax+b的图象上.
(1)用含a的代数式表示b;
(2)如果该二次函数的图象与x轴只有一个交点,求这个二次函数的图象的顶点坐标
已知抛物线y=ax2+bx+c经过A(-4,3)、B(2,0)两点,当x=3和x=-3时,这条抛物线上对应点的纵坐标相等.经过点C(0,-2)的直线l与 x轴平行,O为坐标原点.
(1)求直线AB和这条抛物线的解析式;
(2)以A为圆心,AO为半径的圆记为⊙A,判断直线l与⊙A的位置关系,并说明理由;
(3)设直线AB上的点D的横坐标为-1,P(m,n)是抛物线y=ax2+bx+c上的动点,当△PDO的周长最小时,求四边形CODP的面积.
(本题满分9分)
如图,以 为顶点的抛物线与
为顶点的抛物线与 轴交于点
轴交于点 .已知
.已知 、
、 两点坐标分别为(3,0)、(0,4).
两点坐标分别为(3,0)、(0,4).
(1)求抛物线的解析式;
(2)设 是抛物线上的一点(
是抛物线上的一点( 、
、 为正整数),且它位于对称轴的右侧.若以
为正整数),且它位于对称轴的右侧.若以 、
、 、
、 、
、 为顶点的四边形四条边的长度是四个连续的正整数,求点
为顶点的四边形四条边的长度是四个连续的正整数,求点 的坐标;
的坐标;
(3)在(2)的条件下,试问:对于抛物线对称轴上的任意一点 ,
, 是否总成立?请说明理由.
是否总成立?请说明理由.
如图,二次函数 的图象经过点D
的图象经过点D ,与x轴交于A、B两点.
,与x轴交于A、B两点.
⑴求 的值;
的值;
⑵如图①,设点C为该二次函数的图象在x轴上方的一点,直线AC将四边形ABCD的面积二等分,试证明线段BD被直线AC平分,并求此时直线AC的函数解析式;
⑶设点P、Q为该二次函数的图象在x轴上方的两个动点,试猜想:是否存在这样的点P、Q,使△AQP≌△ABP?如果存在,请举例验证你的猜想;如果不存在,请说明理由.
(图②供选用)
(本小题满分9分)
如图,已知二次函数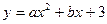 的图象与x轴相交于点A、C,与y轴交于点B,A(
的图象与x轴相交于点A、C,与y轴交于点B,A(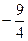 ,0),且△AOB~△BOC。
,0),且△AOB~△BOC。
(1)求C点坐标、∠ABC的度数及二次函数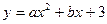 的关系式;
的关系式;
(2)在线段AC上是否存在点M(m,0),使得以线段BM为直径的圆与边BC交于P点(与点B不同),且以点P、C、O为顶点的三角形是等腰三角形?若存在,求出m的值;若不存在,请说明理由
抛物线 经过A(
经过A(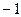 ,0)、C(0,
,0)、C(0,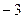 )两点,与
)两点,与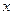 轴交于另一点B。
轴交于另一点B。
(1)求此抛物线的解析式;
(2)已知点D(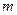 ,
,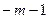 )在第四象限的抛物线上,求点D关于直线BC对称的点
)在第四象限的抛物线上,求点D关于直线BC对称的点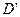 ,的坐标。
,的坐标。
(3)在(2)的条件下,连结BD,问在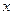 轴上是否存在点P,使
轴上是否存在点P,使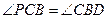 ,若存在,请求出P点的坐标;若不存在,请说明理由
,若存在,请求出P点的坐标;若不存在,请说明理由
某公司推出一款新型手机,投放市场以来前3个月的利润情况如图所示,该图可以近似看作抛物线的一部分。请结合图象,解答以下问题:
(1)求该抛物线对应的二次函数解析式;
(2)该公司在经营此款手机过程中,第几月的利润能达到24万元?
(3)若照此经营下去,请你结合所学的知识,对公司在此款手机的经营状况(是否亏损?何时亏损?)作预测分析