2011届上海市奉贤区初三上学期期末第一次模拟数学卷
用一根长80 的绳子围成一个长方形,且长方形的长比宽长10
的绳子围成一个长方形,且长方形的长比宽长10 ,则这个长方形的面积是( )
,则这个长方形的面积是( )
A.25 |
B.45 |
C.375 |
D.1575 |
下表,填在各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )
| A.38 | B.52 | C.66 | D.74 |
“激情盛会,和谐亚洲”第16届亚运会在中国广州举行,广州亚运城的建筑面积约是358000平方米,将358000用科学记数法表示为____________
如图所示,AB=4 cm.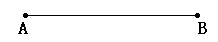
(1)画图,延长AB到C,使BC=3 cm.
(2)如果点D是线段AB的中点,点E是线段BC的中点,那么线段DE的长度是多少?
如图,正方形网格的边长为1点P是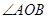 的边OB上的一点。
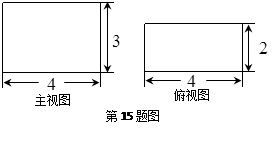
的边OB上的一点。
过点P画OB的垂线,交OA于点C;
过点P画OA的垂线,垂足为H;
点P到OA的距离为__________,因为直线外一点到直线上各点连接的所有线中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是 。(用“<”号连接)
城区某新建住宅小区计划购买并种植甲、乙两种树苗共300株.已知甲种树苗每株60元,乙种树苗每株90元.
(1)若购买树苗共用21000元,问甲、乙两种树苗应各买多少株?
(2)据统计,甲、乙两种树苗每株树苗对空气的净化指数分别为 和
和 ,问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和等于90?
,问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和等于90?
有一列数,第一个数为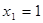 ,第二个数为
,第二个数为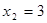 ,从第三个数开始依次为
,从第三个数开始依次为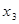 ,
,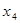 ,…
,…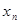 ,从第二个数开始,每个数是左右相邻两个数和的一半,如:
,从第二个数开始,每个数是左右相邻两个数和的一半,如: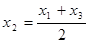 .
.
(1)求第三、第四、第五个数,并写出计算过程;
(2)根据(1)的结果,推测 =_______________;
=_______________;
(3)探索这一列数的规律,猜想第k个数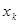 =_______________
=_______________
如图,将正方形纸片的两角分别折叠,使顶点A落在A′处,顶点D落在D′处,BC、BE为折痕,点B、A′、D′在同一条直线上。
(1)猜想折痕BC和BE的位置关系,并说明理由;
(2)写出图中∠D′BE的余角与补角;
(3)延长D′B、CA相交于点F,若∠EBD=330,求∠ABF和∠CBA的度数。
如图,将连续奇数1,3,5,7,…排成如下数表,观察十字框内5个数,探索这五个数之间的规律,解答下面的问题:
| 1 |
3 |
5 |
7 |
9 |
11 |
| 13 |
15 |
17 |
19 |
21 |
23 |
| 25 |
27 |
29 |
31 |
33 |
35 |
| 37 |
39 |
41 |
43 |
45 |
47 |
| … |
|
|
|
|
|
(1)设十字框中间的数为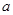 ,请用含
,请用含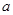 的式子表示十字框内5个数的和为
的式子表示十字框内5个数的和为
(2)十字框内5个数的和能等于2010吗?若能,请求出框内5个数;若不能,请说明理由;
(3)十字框内5个数的和能等于2015吗?若能,请求出框内5个数;若不能,请说明理由;
自上海世博会开幕以来,中国馆以其独特的造型吸引了世人的目光.据统计,在会展期间,参观中国馆的人次数达到14 900 000,此数用科学记数法表示是
A. |
B. |
C. |
D. |
二次函数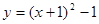 图象的顶点坐标是
图象的顶点坐标是
| A.(1,1); | B.(1,-1); | C.(-1,1); | D.(-1,-1) |
已知线段a、b,且 ,那么下列说法错误的是
,那么下列说法错误的是
| A.a=2cm,b=3cm; | B.a=2 k,b=3 k (k>0); |
| C.3a=2b ; | D. . . |
下列语句错误的是
A.如果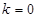 或 或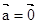 ,那么 ,那么 ; ; |
B.如果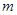 、 、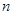 为实数,那么 为实数,那么 ; ; |
C.如果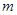 、 、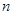 为实数,那么 为实数,那么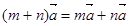 ; ; |
D.如果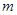 、 、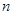 为实数,那么 为实数,那么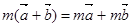 . . |
如果点D、E分别在△ABC边AB、AC的反向延长线上,一定能推出DE∥BC的条件是
A. ; B.
; B. ; C.
; C. ; D.
; D. .
.
下列图形中一定相似的一组是
| A.邻边对应成比例的两个平行四边形; | B.有一个内角相等的两个菱形; |
| C.腰长对应成比例的两个等腰三角形; | D.有一条边相等的两个矩形 |
上海与南京的实际距离约350千米,在比例尺为1:5 000 000的地图上,上海与南京的图上距离约 ▲ 厘米.
已知二次函数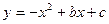 的图像经过A(-1,-6)、B(2,-3),求这个函数的解析式及这个函数图像的顶点坐标
的图像经过A(-1,-6)、B(2,-3),求这个函数的解析式及这个函数图像的顶点坐标
如图:AD//EG//BC,EG分别交AB、DB、AC于点E、F、G,已知AD=6,BC=10,AE=3,AB=5,求EG、FG的长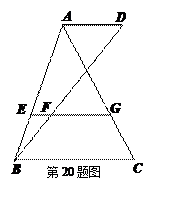
随着本区近几年城市建设的快速发展,对花木的需求量逐年提高。某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润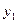 与投资量
与投资量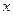 成正比例关系,如图(1)所示;种植花卉的利润
成正比例关系,如图(1)所示;种植花卉的利润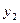 与投资量
与投资量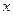 成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)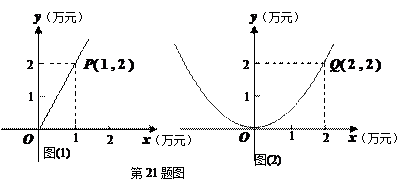
如图,河流两岸a,b互相平行,C,D是河岸a上间隔50米的两个电线杆.小英在河岸b上的A处测得∠DAB=30°,然后沿河岸走了100米到达B处,测得∠CBM=60°,求河流的宽度.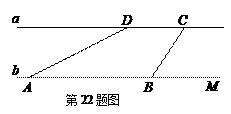
已知Rt△ABC中,∠ACB=90°中,AC=2,BC=4,点D在BC边上,且∠CAD=∠B.
(1) 求AD的长.
(2) 取AD、AB的中点E、F,联结CE、CF、EF,求证:△CEF∽△ADB.
如图,已知抛物线与 轴交于点
轴交于点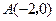 ,
,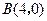 ,与y轴交于点
,与y轴交于点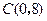 .
.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交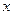 轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
如图,直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=2DC=4,AB=6.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
(1)当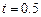 时,求线段
时,求线段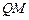 的长;
的长;
(2)点M在线段AB上运动时,是否可以使得以C、P、Q为顶点的三角形为直角三角形,若可以,请直接写出t的值(不需解题步骤);若不可以,请说明理由.
(3)若△PCQ的面积为y,请求y关于出t 的函数关系式及自变量的取值范围;
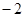 为解的一元一次方程为
为解的一元一次方程为 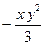 的系数是___
的系数是___ 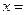 时,代数式
时,代数式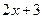 与
与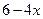 的值相等
的值相等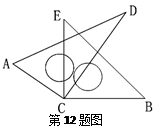
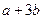 的值为
的值为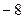 ,则代数式
,则代数式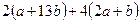 的值为_________
的值为_________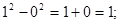

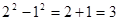 ;
; 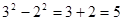 ;
;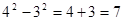 ;
; 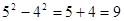 ; ……
; ……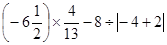
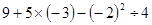

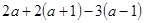
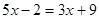
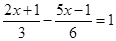
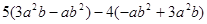 ,其中
,其中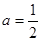 ,
,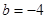
 +3
+3
 =3
=3
 -3
-3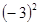 与
与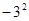
 与
与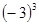 与
与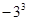

 与
与  是∠B的
是∠B的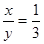 ,那么
,那么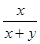 = ▲
= ▲ = ▲
= ▲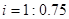 ,一物体由斜面底部沿斜面向前推了10米,那么这个物体升高了 ▲ 米.
,一物体由斜面底部沿斜面向前推了10米,那么这个物体升高了 ▲ 米. ,它的图像在对称轴 ▲ (填“左侧”或“右侧”)的部分是下降的
,它的图像在对称轴 ▲ (填“左侧”或“右侧”)的部分是下降的 的对称轴是y轴,那么b的值为 ▲
的对称轴是y轴,那么b的值为 ▲ 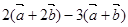 = ▲
= ▲  ,那么用向量
,那么用向量 表示向量
表示向量 为 ▲
为 ▲ 
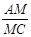 的值是 ▲ .
的值是 ▲ . 粤公网安备 44130202000953号
粤公网安备 44130202000953号