将一物体(视为边长为 米的正方形 从地面 上挪到货车车厢内.如图所示,刚开始点 与斜面 上的点 重合,先将该物体绕点 (E)按逆时针方向旋转至正方形 的位置,再将其沿 方向平移至正方形 的位置(此时点 与点 重合),最后将物体移到车厢平台面 上.已知 , ,过点 作 于点 , 米, 米.
(1)求线段 的长度;
(2)求在此过程中点 运动至点 所经过的路程.

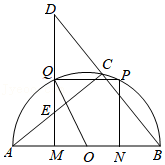
如图,点 为以 为直径的半圆的圆心,点 , 在直径 上,点 , 在 上,四边形 为正方形,点 在 上运动(点 与点 , 不重合),连接 并延长交 的延长线于点 ,连接 交 于点 ,连接 .
(1)求 的值;
(2)求 的值;
(3)令 , ,直径 , 是常数),求 关于 的函数解析式,并指明自变量 的取值范围.
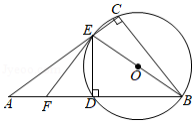
如图,在 中, , ,以点 为圆心, 为半径的圆交 的延长线于点 ,过点 作 的平行线,交 于点 ,连接 .
(1)求证: 为 的切线;
(2)若 ,求弧 的长.

如图,正方形 内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称,设正方形 的面积为 ,黑色部分面积为 ,则 的比值为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, , 的垂直平分线分别交 、 于点 、 , , 为 的外接圆,过点 作 的切线 交 于点 ,则下列结论正确的是 (写出所有正确结论的序号)
① ;
② ;
③若 ,则 的长为 ;
④ ;
⑤若 ,则 .
如图1, 是 的直径,点 是 上一动点,且不与 , 两点重合, 的平分线交 于点 ,过点 作 ,交 的延长线于点 .

(1)求证: 是 的切线;
(2)求证: ;
(3)如图2,原有条件不变,连接 , ,延长 至点 , 的平分线交 的延长线于点 , 的平分线交 的平分线于点 .求证:无论点 如何运动,总有 .
某同学在数学实践活动中,制作了一个侧面积为 ,底面半径为6的圆锥模型(如图所示),则此圆锥的母线长为 .

某种冰激凌的外包装可以视为圆锥,它的底面圆直径 与母线 长之比为 .制作这种外包装需要用如图所示的等腰三角形材料,其中 , .将扇形 围成圆锥时, , 恰好重合.
(1)求这种加工材料的顶角 的大小.
(2)若圆锥底面圆的直径 为 ,求加工材料剩余部分(图中阴影部分)的面积.(结果保留
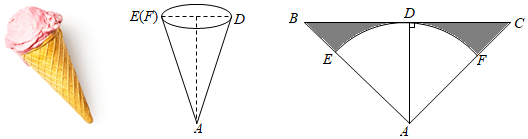
如图,点 在以 为直径的 上, 的角平分线与 相交于点 ,与 相交于点 ,延长 至 ,连结 ,使得 ,过点 作 的平行线与 的延长线交于点 .
(1)求证: 与 相切;
(2)试给出 、 、 之间的数量关系,并予以证明.

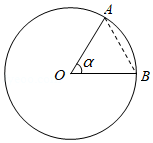
弧度是表示角度大小的一种单位,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作 .已知 , ,则 与 的大小关系是 .