初中数学函数的图象试题

均匀地向一个容器内注水，在注满水的过程中，水面的高度 $h$ 与时间 $t$ 的函数关系如图所示，则该容器是下列四个中的 $($ 　　 $)$

A．

B．

C．

D．

爷爷在离家900米的公园锻炼后回家，离开公园20分钟后，爷爷停下来与朋友聊天10分钟，接着又走了15分钟回到家中．下面图形中表示爷爷离家的距离 $y$ （米 $)$ 与爷爷离开公园的时间 $x$ （分 $)$ 之间的函数关系是 $($ 　　 $)$

A．		B．
C．		D．

如图1，在四边形中，，，直线．当直线沿射线方向，从点开始向右平移时，直线与四边形的边分别相交于点、．设直线向右平移的距离为，线段的长为，且与的函数关系如图2所示，则四边形的周长是　　．

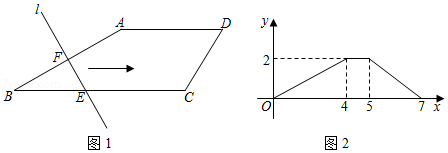
某农作物的生长率与温度有如下关系：如图1，当时可近似用函数刻画；当时可近似用函数刻画．

（1）求的值．

（2）按照经验，该作物提前上市的天数（天与生长率满足函数关系：

生长率	0.2	0.25	0.3	0.35
提前上市的天数（天	0	5	10	15

①请运用已学的知识，求关于的函数表达式；

②请用含的代数式表示．

（3）天气寒冷，大棚加温可改变农作物生长速度．在（2）的条件下，原计划大棚恒温时，每天的成本为200元，该作物30天后上市时，根据市场调查：每提前一天上市售出（一次售完），销售额可增加600元．因此给大棚继续加温，加温后每天成本（元与大棚温度之间的关系如图2．问提前上市多少天时增加的利润最大？并求这个最大利润（农作物上市售出后大棚暂停使用）．

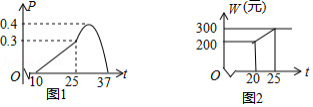
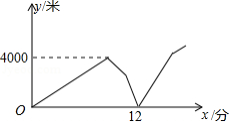
某公司快递员甲匀速骑车前往某小区送物件，出发几分钟后，快递员乙发现甲的手机落在公司，无法联系，于是乙匀速骑车去追赶甲．乙刚出发2分钟时，甲也发现自己手机落在公司，立刻按原路原速骑车回公司，2分钟后甲遇到乙，乙把手机给甲后立即原路原速返回公司，甲继续原路原速赶往某小区送物件，甲乙两人相距的路程（米与甲出发的时间（分钟）之间的关系如图所示（乙给甲手机的时间忽略不计）．则乙回到公司时，甲距公司的路程是　　米．

一天早晨，小玲从家出发匀速步行到学校，小玲出发一段时间后，她的妈妈发现小玲忘带了一件必需的学习用品，于是立即下楼骑自行车，沿小玲行进的路线，匀速去追小玲，妈妈追上小玲将学习用品交给小玲后，立即沿原路线匀速返回家里，但由于路上行人渐多，妈妈返回时骑车的速度只是原来速度的一半，小玲继续以原速度步行前往学校，妈妈与小玲之间的距离（米与小玲从家出发后步行的时间（分之间的关系如图所示（小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计）．当妈妈刚回到家时，小玲离学校的距离为　　米．

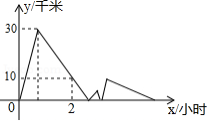
，两地相距的路程为240千米，甲、乙两车沿同一线路从地出发到地，分别以一定的速度匀速行驶．甲车先出发40分钟后，乙车才出发．途中乙车发生故障，修车耗时20分钟，随后，乙车车速比发生故障前减少了10千米小时（仍保持匀速前行），甲、乙两车同时到达地．甲、乙两车相距的路程（千米）与甲车行驶时间（小时）之间的关系如图所示，求乙车修好时，甲车距地还有　　千米．

甲、乙两人在一条笔直的道路上相向而行，甲骑自行车从地到地，乙驾车从地到地，他们分别以不同的速度匀速行驶，已知甲先出发6分钟后，乙才出发，在整个过程中，甲、乙两人的距离（千米）与甲出发的时间（分之间的关系如图所示，当乙到达终点时，甲还需　　分钟到达终点．

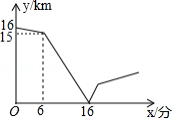
周末，扎西到南山公园爬山，他从山脚爬到山顶的途中，休息了一段时间．设他从山脚出发后所用时间为 $t$ （分钟），所走的路程为 $s$ （米 $)$ ， $s$ 与 $t$ 之间的函数关系如图所示．下列说法错误的是 $($ 　　 $)$

A．	扎西中途休息了20分钟
B．	扎西休息前爬山的平均速度为每分钟70米
C．	扎西在上述过程中所走的路程为6600米
D．	扎西休息前爬山的平均速度大于休息后爬山的平均速度

数学活动课上，张老师引导同学进行如下探究：

如图1，将长为的铅笔斜靠在垂直于水平桌面的直尺的边沿上，一端固定在桌面上，图2是示意图．

活动一

如图3，将铅笔绕端点顺时针旋转，与交于点，当旋转至水平位置时，铅笔的中点与点重合．

数学思考

（1）设，点到的距离．

①用含的代数式表示：的长是　　，的长是　　；

②与的函数关系式是　　，自变量的取值范围是　　．

活动二

（2）①列表：根据（1）中所求函数关系式计算并补全表格

	6	5	4	3.5	3	2.5	2	1	0.5	0
	0	0.55	1.2	1.58		2.47	3	4.29	5.08

②描点：根据表中数值，继续描出①中剩余的两个点．

③连线：在平面直角坐标系中，请用平滑的曲线画出该函数的图象．

数学思考

（3）请你结合函数的图象，写出该函数的两条性质或结论．

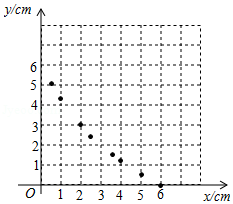
某校拟建一个面积为 $100m^2$ 的矩形健身区，张老师请同学们小组合作设计出使周长最小的建造方案，下面是其中一个小组的探究过程，请补充完整

（1）列式

设矩形的一边长是 $\mathit{xm}$ ，则另一边长是 　　 $m$ ，若周长为 $\mathit{ym}$ ，则 $y$ 与 $x$ 之间的函数关系式为 　　

（2）画图

①列表

$x$	$\dots$	4	6	10	13	16	20	25	30	$\dots$
$y$	$\dots$	58	$45\frac{1}{3}$	40	$41\frac{5}{13}$	$44\frac{1}{2}$	$a$	58	$66\frac{2}{3}$	$\dots$

表中 $a=$ 　　

②描点：如图所示；

③连线：请在图中画出该函数的图象．

（3）发现

图象最低点的坐标为 　　，即当 $x=$ 　　 $m$ 时，周长 $y$ 有最小值 $40m$ ；

（4）验证

在张老师的指导下，同学们将 $y$ 与 $x$ 之间的函数关系式进行配方，得出 $y=2{(\sqrt{x}-\frac{10}{\sqrt{x}})}^2+40$ ．

$\because 2{(\sqrt{x}-\frac{10}{\sqrt{x}})}^2⩾0$

$\therefore y⩾$ 　　．

$\therefore$ 当 $\sqrt{x}-\frac{10}{\sqrt{x}}=0$ 时， $y$ 有最小值；

此方程可化为 ${\left(\sqrt{x}\right)}^2-10=0$ ；

$\therefore$ 当 $x=$ 　　 $m$ 时，周长 $y$ 有最小值 $40m$ ．

小苏和小林在如图1所示的跑道上进行 $4\times 50$ 米折返跑．在整个过程中，跑步者距起跑线的距离 $y$ （单位： $m)$ 与跑步时间 $t$ （单位： $s)$ 的对应关系如图2所示．下列叙述正确的是 $($ 　　 $)$

A．	两人从起跑线同时出发，同时到达终点
B．	小苏跑全程的平均速度大于小林跑全程的平均速度
C．	小苏前 $15s$ 跑过的路程大于小林前 $15s$ 跑过的路程
D．	小林在跑最后 $100m$ 的过程中，与小苏相遇2次

已知 $y$ 是 $x$ 的函数，自变量 $x$ 的取值范围 $x>0$ ，下表是 $y$ 与 $x$ 的几组对应值：

$x$	$\dots$	1	2	3	5	7	9	$\dots$
$y$	$\dots$	1.98	3.95	2.63	1.58	1.13	0.88	$\dots$

小腾根据学习函数的经验，利用上述表格所反映出的 $y$ 与 $x$ 之间的变化规律，对该函数的图象与性质进行了探究．

下面是小腾的探究过程，请补充完整：

（1）如图，在平面直角坐标系 $\mathit{xOy}$ 中，描出了以上表格中各对对应值为坐标的点，根据描出的点，画出该函数的图象；

（2）根据画出的函数图象，写出：

① $x=4$ 对应的函数值 $y$ 约为 　 　；

②该函数的一条性质： 　　．

在 $1-7$ 月份，某种水果的每斤进价与售价的信息如图所示，则出售该种水果每斤利润最大的月份是 $($ 　　 $)$

A．

3月份

B．

4月份

C．

5月份

D．

6月份

小丽一家利用元旦三天驾车到某景点旅游.小汽车出发前油箱有油36L，行驶若干h后，途中在加油站加油若干L.油箱中余油量Q（L）与行驶时间t（h）之间的关系如图所示。根据图象回答下列问题：

（1）小汽车行驶________h后加油, 中途加油__________L；
（2）求加油前油箱余油量Q与行驶时间t的函数关系式；
（3）如果加油站距景点200km，车速为80km/h，要到达目的地，油箱中的油是否够用？请说明理由.