初中数学函数的图象解答题

在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质及其应用的过程．以下是我们研究函数 $y=\frac{4-x^2}{x^2+1}$ 的性质及其应用的部分过程，请按要求完成下列各小题．

（1）请把下表补充完整，并在给出的图中补全该函数的大致图象；

$x$	$\dots$	$-5$	$-4$	$-3$	$-2$	$-1$	0	1	2	3	4	5	$\dots$
$y=\frac{4-x^2}{x^2+1}$	$\dots$	$-\frac{21}{26}$	$-\frac{12}{17}$	$-\frac{1}{2}$	0	$\frac{3}{2}$	4	$\frac{3}{2}$	0				$\dots$

（2）请根据这个函数的图象，写出该函数的 $\text{"}D$ 条性质；

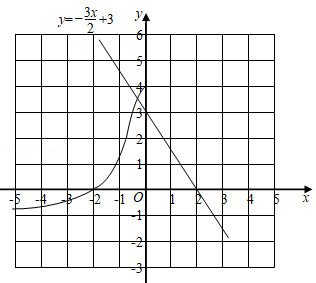
（3）已知函数 $y=-\frac{3}{2}x+3$ 的图象如图所示．根据函数图象，直接写出不等式 $-\frac{3}{2}x+3>\frac{4-x^2}{x^2+1}$ 的解集．（近似值保留一位小数，误差不超过 $0.2)$

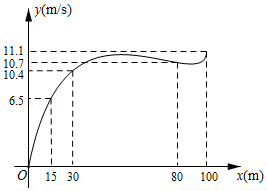
根据数学家凯勒的"百米赛跑数学模型"，前30米称为"加速期"，30米 $~80$ 米为"中途期"，80米 $~100$ 米为"冲刺期"．市田径队把运动员小斌某次百米跑训练时速度 $y(m/s)$ 与路程 $x\left(m\right)$ 之间的观测数据，绘制成曲线如图所示．

（1） $y$ 是关于 $x$ 的函数吗？为什么？

（2）"加速期"结束时，小斌的速度为多少？

（3）根据如图提供的信息，给小斌提一条训练建议．

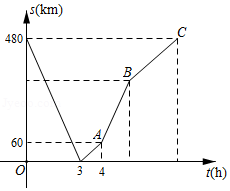
在"看图说故事"活动中，某学习小组结合图象设计了一个问题情境．已知学校、书店、陈列馆依次在同一条直线上，书店离学校 $12\mathit{km}$ ，陈列馆离学校 $20\mathit{km}$ ．李华从学校出发，匀速骑行 $0.6h$ 到达书店；在书店停留 $0.4h$ 后，匀速骑行 $0.5h$ 到达陈列馆；在陈列馆参观学习一段时间，然后回学校；回学校途中，匀速骑行 $0.5h$ 后减速，继续匀速骑行回到学校．给出的图象反映了这个过程中李华离学校的距离 $y\mathit{km}$ 与离开学校的时间 $xh$ 之间的对应关系．

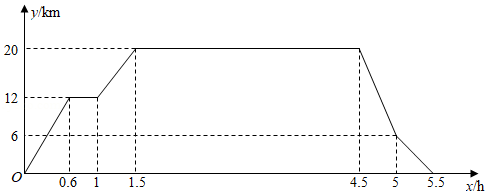
请根据相关信息，解答下列问题：

（Ⅰ）填表：

离开学校的时间     $/h$	0.1	0.5	0.8	1	3
离学校的距离     $/\mathit{km}$	2	10		12

（Ⅱ）填空：

①书店到陈列馆的距离为 　　 $\mathit{km}$ ；

②李华在陈列馆参观学习的时间为 　　 $h$ ；

③李华从陈列馆回学校途中，减速前的骑行速度为 　　 $\mathit{km}/h$ ；

④当李华离学校的距离为 $4\mathit{km}$ 时，他离开学校的时间为 　　 $h$ ．

（Ⅲ）当 $0⩽x⩽1.5$ 时，请直接写出 $y$ 关于 $x$ 的函数解析式．

函数图象是研究函数的重要工具。探究函数性质时，我们经历了列表、描点、连线画出函数图象，然后观察分析图象特征，概括函数性质的过程。请结合已有的学习经验，画出函数 $y=-\frac{8x}{x^2+4}$ 的图象，并探究其性质．

列表如下：

$x$	$\dots$	$-4$	$-3$	$-2$	$-1$	0	1	2	3	4	$\dots$
$y$	$\dots$	$\frac{8}{5}$	$\frac{24}{13}$	$a$	$\frac{8}{5}$	0	$b$	$-2$	$-\frac{24}{13}$	$-\frac{8}{5}$	$\dots$

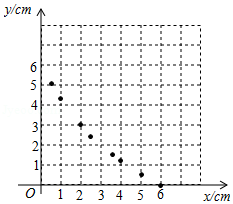
（1）写出表中 $a$ 、 $b$ 的值，并在平面直角坐标系中画出该函数的图象；

（2）观察函数 $y=-\frac{8x}{x^2+4}$ 的图象，判断下列关于该函数性质的命题：

①当 $-2⩽x⩽2$ 时，函数图象关于直线 $y=x$ 对称；

② $x=2$ 时，函数有最小值，最小值为 $-2$ ；

③ $-1<x<1$ 时，函数 $y$ 的值随 $x$ 的增大而减小．

其中正确的是 　　．（请写出所有正确命题的番号）

（3）结合图象，请写出不等式 $\frac{8x}{x^2+4}>x$ 的解集 　　．

已知函数 $y=\left\{\begin{array}{c}\frac{3}{x},x⩽-1,\\ 3x,-1<x⩽1,\\ \frac{3}{x},x⩾1\cdot \end{array}\right.$

（1）画出函数图象；

列表：

$x$	$\dots$	$-3$								$\dots$
$y$	$\dots$									$.\dots$

描点，连线得到函数图象：

（2）该函数是否有最大或最小值？若有，求出其值，若没有，简述理由；

（3）设 $(x_1$， $y_1)$， $(x_2$， $y_2)$是函数图象上的点，若 $x_1+x_2=0$，证明： $y_1+y_2=0$．

一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶，两车在途中相遇时，快车恰巧出现故障，慢车继续驶往甲地，快车维修好后按原速继续行驶乙地，两车到达各地终点后停止，两车之间的距离 $s\left(\mathit{km}\right)$ 与慢车行驶的时间 $t\left(h\right)$ 之间的关系如图：

（1）快车的速度为 　　 $\mathit{km}/h$ ， $C$ 点的坐标为 　　．

（2）慢车出发多少小时后，两车相距 $200\mathit{km}$ ．

小欣在学习了反比例函数的图象与性质后，进一步研究了函数 $y=\frac{1}{x+1}$的图象与性质．其研究过程如下：

（1）绘制函数图象

①列表：如表是 $x$与 $y$的几组对应值，其中 $m=$　　；

$x$	$\dots$	$-4$	$-3$	$-2$	$-\frac{3}{2}$	$-\frac{4}{3}$	$-\frac{2}{3}$	$-\frac{1}{2}$	0	1	2	$\dots$
$y$	$\dots$	$-\frac{1}{3}$	$-\frac{1}{2}$	$-1$	$-2$	$-3$	3	2	$m$	$\frac{1}{2}$	$\frac{1}{3}$	$\dots$

②描点：根据表中的数值描点 $(x,y)$，请补充描出点 $(0,m)$；

③连线：用平滑的曲线顺次连接各点，请把图象补充完整．

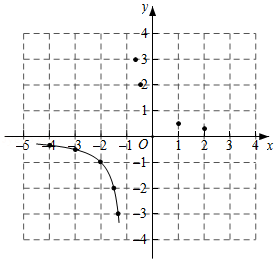
（2）探究函数性质

判断下列说法是否正确（正确的填“ $\surd$”，错误的填“ $\times$” $)$

①函数值 $y$随 $x$的增大而减小：　　．

②函数图象关于原点对称：　　．

③   函数图象与直线 $x=-1$没有交点：　　．

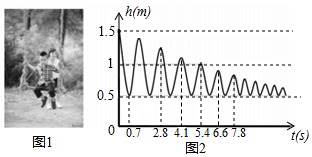
小红帮弟弟荡秋千（如图 $1)$，秋千离地面的高度 $ℎ\left(m\right)$与摆动时间 $t\left(s\right)$之间的关系如图2所示．

（1）根据函数的定义，请判断变量 $ℎ$是否为关于 $t$的函数？

（2）结合图象回答：

①当 $t=0.7s$时， $ℎ$的值是多少？并说明它的实际意义．

②秋千摆动第一个来回需多少时间？

某周日上午 $8:00$小宇从家出发，乘车1小时到达某活动中心参加实践活动． $11:00$时他在活动中心接到爸爸的电话，因急事要求他在 $12:00$前回到家，他即刻按照来活动中心时的路线，以5千米 $/$小时的平均速度快步返回．同时，爸爸从家沿同一路线开车接他，在距家20千米处接上了小宇，立即保持原来的车速原路返回．设小宇离家 $x$（小时）后，到达离家 $y$（千米）的地方，图中折线 $\mathit{OABCD}$表示 $y$与 $x$之间的函数关系．

（1）活动中心与小宇家相距　   　千米，小宇在活动中心活动时间为　 　小时，他从活动中心返家时，步行用了　    　小时；

（2）求线段 $\mathit{BC}$所表示的 $y$（千米）与 $x$（小时）之间的函数关系式（不必写出 $x$所表示的范围）；

（3）根据上述情况（不考虑其他因素），请判断小宇是否能在 $12:00$前回到家，并说明理由．

甲车从地驶往地，同时乙车从地驶往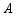地，两车相向而行，匀速行驶，甲车距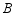地的距离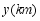与行驶时间之间的函数关系如图所示，乙车的速度是

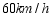
（1）求甲车的速度；

（2）当甲乙两车相遇后，乙车速度变为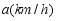，并保持匀速行驶，甲车速度保持不变，结果乙车比甲车晚38分钟到达终点，求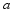的值．

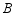甲车从地驶往地，同时乙车从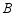地驶往地，两车相向而行，匀速行驶，甲车距地的距离与行驶时间之间的函数关系如图所示，乙车的速度是

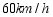
（1）求甲车的速度；

（2）当甲乙两车相遇后，乙车速度变为，并保持匀速行驶，甲车速度保持不变，结果乙车比甲车晚38分钟到达终点，求的值．

通过课本上对函数的学习，我们积累了一定的经验．下表是一个函数的自变量与函数值的部分对应值，请你借鉴以往学习函数的经验，探究下列问题：

		0	1	2	3	4	5
		6	3	2	1.5	1.2	1

（1）当　　时，；

（2）根据表中数值描点，并画出函数图象；

（3）观察画出的图象，写出这个函数的一条性质：　　．

某农作物的生长率与温度有如下关系：如图1，当时可近似用函数刻画；当时可近似用函数刻画．

（1）求的值．

（2）按照经验，该作物提前上市的天数（天与生长率满足函数关系：

生长率	0.2	0.25	0.3	0.35
提前上市的天数（天	0	5	10	15

①请运用已学的知识，求关于的函数表达式；

②请用含的代数式表示．

（3）天气寒冷，大棚加温可改变农作物生长速度．在（2）的条件下，原计划大棚恒温时，每天的成本为200元，该作物30天后上市时，根据市场调查：每提前一天上市售出（一次售完），销售额可增加600元．因此给大棚继续加温，加温后每天成本（元与大棚温度之间的关系如图2．问提前上市多少天时增加的利润最大？并求这个最大利润（农作物上市售出后大棚暂停使用）．

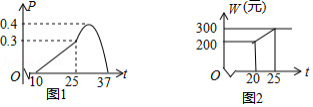
数学活动课上，张老师引导同学进行如下探究：

如图1，将长为的铅笔斜靠在垂直于水平桌面的直尺的边沿上，一端固定在桌面上，图2是示意图．

活动一

如图3，将铅笔绕端点顺时针旋转，与交于点，当旋转至水平位置时，铅笔的中点与点重合．

数学思考

（1）设，点到的距离．

①用含的代数式表示：的长是　　，的长是　　；

②与的函数关系式是　　，自变量的取值范围是　　．

活动二

（2）①列表：根据（1）中所求函数关系式计算并补全表格

	6	5	4	3.5	3	2.5	2	1	0.5	0
	0	0.55	1.2	1.58		2.47	3	4.29	5.08

②描点：根据表中数值，继续描出①中剩余的两个点．

③连线：在平面直角坐标系中，请用平滑的曲线画出该函数的图象．

数学思考

（3）请你结合函数的图象，写出该函数的两条性质或结论．

某校拟建一个面积为 $100m^2$ 的矩形健身区，张老师请同学们小组合作设计出使周长最小的建造方案，下面是其中一个小组的探究过程，请补充完整

（1）列式

设矩形的一边长是 $\mathit{xm}$ ，则另一边长是 　　 $m$ ，若周长为 $\mathit{ym}$ ，则 $y$ 与 $x$ 之间的函数关系式为 　　

（2）画图

①列表

$x$	$\dots$	4	6	10	13	16	20	25	30	$\dots$
$y$	$\dots$	58	$45\frac{1}{3}$	40	$41\frac{5}{13}$	$44\frac{1}{2}$	$a$	58	$66\frac{2}{3}$	$\dots$

表中 $a=$ 　　

②描点：如图所示；

③连线：请在图中画出该函数的图象．

（3）发现

图象最低点的坐标为 　　，即当 $x=$ 　　 $m$ 时，周长 $y$ 有最小值 $40m$ ；

（4）验证

在张老师的指导下，同学们将 $y$ 与 $x$ 之间的函数关系式进行配方，得出 $y=2{(\sqrt{x}-\frac{10}{\sqrt{x}})}^2+40$ ．

$\because 2{(\sqrt{x}-\frac{10}{\sqrt{x}})}^2⩾0$

$\therefore y⩾$ 　　．

$\therefore$ 当 $\sqrt{x}-\frac{10}{\sqrt{x}}=0$ 时， $y$ 有最小值；

此方程可化为 ${\left(\sqrt{x}\right)}^2-10=0$ ；

$\therefore$ 当 $x=$ 　　 $m$ 时，周长 $y$ 有最小值 $40m$ ．