函数图象是研究函数的重要工具。探究函数性质时,我们经历了列表、描点、连线画出函数图象,然后观察分析图象特征,概括函数性质的过程。请结合已有的学习经验,画出函数 的图象,并探究其性质.
列表如下:
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
(1)写出表中 、 的值,并在平面直角坐标系中画出该函数的图象;
(2)观察函数 的图象,判断下列关于该函数性质的命题:
①当 时,函数图象关于直线 对称;
② 时,函数有最小值,最小值为 ;
③ 时,函数 的值随 的增大而减小.
其中正确的是 .(请写出所有正确命题的番号)
(3)结合图象,请写出不等式 的解集 .

推荐套卷
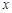 轴、
轴、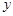 轴于点A(-2,0),B(0,2),点C是直线AB上一点,且∠ACO=30°,求AC的长及点C的坐标.
轴于点A(-2,0),B(0,2),点C是直线AB上一点,且∠ACO=30°,求AC的长及点C的坐标.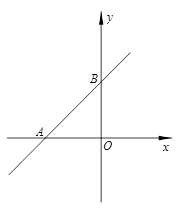
 、
、 的方程组
的方程组 的解满足不等式组
的解满足不等式组 ,求满足条件的
,求满足条件的 的整数值.
的整数值. ,
, ,求代数式
,求代数式 的值.
的值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号