初中数学平面直角坐标系试题

我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，边长为2的正方形 $\mathit{ABCD}$ 的边 $\mathit{AB}$ 在 $x$ 轴上， $\mathit{AB}$ 的中点是坐标原点 $O$ ，固定点 $A$ ， $B$ ，把正方形沿箭头方向推，使点 $D$ 落在 $y$ 轴正半轴上点 $D\text{'}$ 处，则点 $C$ 的对应点 $C\text{'}$ 的坐标为 $($ 　　 $)$

A．

$(\sqrt{3}$ ， $1)$

B．

$(2,1)$

C．

$(1,\sqrt{3})$

D．

$(2,\sqrt{3})$

如图所示，小球从台球桌面 $\mathit{ABCO}$ 上的点 $P(0,1)$ 出发，撞击桌边发生反弹，反射角等于入射角若小球以每秒 $\sqrt{2}$ 个单位长度的速度沿图中箭头方向运动，则第50秒的小球所在位置的坐标为 $($ 　　 $)$

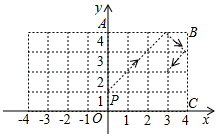
A．

$(2,3)$

B．

$(3,4)$

C．

$(3,2)$

D．

$(0,1)$

如图，正方形 $\mathit{ABCD}$ 的顶点 $B$ 、 $C$ 的坐标分别为 $(0,3)$ ， $(2,0)$ ，则点 $A$ 关于原点 $O$ 的对称点的坐标为 $($ 　　 $)$

A．

$(3,5)$

B．

$(-5,-2)$

C．

$(-3,-5)$

D．

$(2,-5)$

如图， 在平面直角坐标系中，，，以点为圆心，长为半径画弧， 交轴的负半轴于点，则点坐标为　　．

如图，若抛物线 $y=-x^2+3$ 与 $x$ 轴围成封闭区域（边界除外）内整点（点的横、纵坐标都是整数）的个数为 $k$ ，则反比例函数 $y=\frac{k}{x}(x>0)$ 的图象是 $($ 　　 $)$

A．		B．
C．		D．

在平面直角坐标系中，函数的图象经过点，直线与图象交于点，与轴交于点．

（1）求的值；

（2）横、纵坐标都是整数的点叫做整点．记图象在点，之间的部分与线段，，围成的区域（不含边界）为．

①当时，直接写出区域内的整点个数；

②若区域内恰有4个整点，结合函数图象，求的取值范围．

如图是老北京城一些地点的分布示意图．在图中，分别以正东、正北方向为 $x$ 轴、 $y$ 轴的正方向建立平面直角坐标系，有如下四个结论：

①当表示天安门的点的坐标为 $(0,0)$ ，表示广安门的点的坐标为 $(-6,-3)$ 时，表示左安门的点的坐标为 $(5,-6)$ ；

②当表示天安门的点的坐标为 $(0,0)$ ，表示广安门的点的坐标为 $(-12,-6)$ 时，表示左安门的点的坐标为 $(10,-12)$ ；

③当表示天安门的点的坐标为 $(1,1)$ ，表示广安门的点的坐标为 $(-11,-5)$ 时，表示左安门的点的坐标为 $(11,-11)$ ；

④当表示天安门的点的坐标为 $(1.5,1.5)$ ，表示广安门的点的坐标为 $(-16.5,-7.5)$ 时，表示左安门的点的坐标为 $(16.5,-16.5)$ ．

上述结论中，所有正确结论的序号是 $($ 　　 $)$

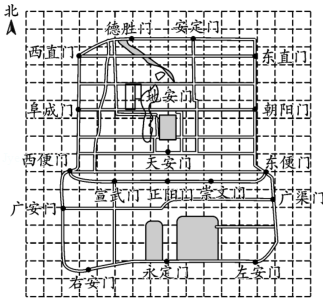
A．

①②③

B．

②③④

C．

①④

D．

①②③④

在平面直角坐标系 $\mathit{xOy}$ 中，点 $P$ 的坐标为 $(x_1$ ， $y_1)$ ，点 $Q$ 的坐标为 $(x_2$ ， $y_2)$ ，且 $x_1\ne x_2$ ， $y_1\ne y_2$ ，若 $P$ ， $Q$ 为某个矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点 $P$ ， $Q$ 的"相关矩形"，如图为点 $P$ ， $Q$ 的"相关矩形"示意图．

（1）已知点 $A$ 的坐标为 $(1,0)$ ，

①若点 $B$ 的坐标为 $(3,1)$ ，求点 $A$ ， $B$ 的"相关矩形"的面积；

②点 $C$ 在直线 $x=3$ 上，若点 $A$ ， $C$ 的"相关矩形"为正方形，求直线 $\mathit{AC}$ 的表达式；

（2） $\odot O$ 的半径为 $\sqrt{2}$ ，点 $M$ 的坐标为 $(m,3)$ ，若在 $\odot O$ 上存在一点 $N$ ，使得点 $M$ ， $N$ 的"相关矩形"为正方形，求 $m$ 的取值范围．

如图，在平面直角坐标系 $\mathit{xOy}$ 中，过点 $A(-6,0)$ 的直线 $l_1$ 与直线 $l_2:y=2x$ 相交于点 $B(m,4)$ ．

（1）求直线 $l_1$ 的表达式；

（2）过动点 $P(n,0)$ 且垂直于 $x$ 轴的直线与 $l_1$ ， $l_2$ 的交点分别为 $C$ ， $D$ ，当点 $C$ 位于点 $D$ 上方时，写出 $n$ 的取值范围．

如图， 直线 $m\perp n$ ，在某平面直角坐标系中， $x$ 轴 $//m$ ， $y$ 轴 $//n$ ，点 $A$ 的坐标为 $(-4,2)$ ，点 $B$ 的坐标为 $(2,-4)$ ，则坐标原点为 $($ 　　 $)$

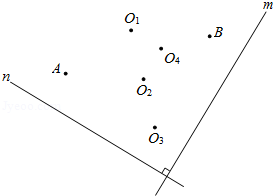
A．

O 1

B．

O 2

C．

O 3

D．

O 4

在平面直角坐标系中，的半径为1，，为外两点，．

给出如下定义：平移线段，得到的弦，分别为点，的对应点），线段长度的最小值称为线段到的“平移距离”．

（1）如图，平移线段得到的长度为1的弦和，则这两条弦的位置关系是　　；在点，，，中，连接点与点　　的线段的长度等于线段到的“平移距离”；

（2）若点，都在直线上，记线段到的“平移距离”为，求的最小值；

（3）若点的坐标为，记线段到的“平移距离”为，直接写出的取值范围．

如图，点A₁（1，0），过A₁作轴的垂线交直线于点B₁，以A₁B₁为边向右作正方形，在轴上一边的另一个端点为A₂，过A₂作轴的长线交直线于点B₂，以A₂B₂为右作正方形…，依次进行下去．

（1）第4个正方形的边长是           ，第5个正方形的边长是          ；
（2）写出点An的坐标．

如图，平面直角坐标系xOy中，点A、B的坐标分别为（3，0）、（2，﹣3），△AB′O′是△ABO关于的A的位似图形，且O′的坐标为（﹣1，0），则点B′的坐标为         ．

如图是学校与小明家位置示意图，如果以学校所在位置为坐标原点，水平方向为x轴建立直角坐标系，那么小明家所在位置的坐标为__________．

如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负。如果从A到B记为：A→B（+1，+3）；从C到D记为：C→D（+1，－2）。其中第一个数表示左右方向，第二个数表示上下方向，那么图中

（1）A→C（   ，   ），C→（-2，   ）；
（2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；
（3）假如这只甲虫从A处去甲虫P处的行走路线依次为
（＋2，＋2），（＋1，－1），（－2，＋3），请在图中标出P的位置．