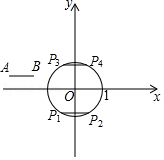
在平面直角坐标系中,的半径为1,,为外两点,.
给出如下定义:平移线段,得到的弦,分别为点,的对应点),线段长度的最小值称为线段到的“平移距离”.
(1)如图,平移线段得到的长度为1的弦和,则这两条弦的位置关系是 ;在点,,,中,连接点与点 的线段的长度等于线段到的“平移距离”;
(2)若点,都在直线上,记线段到的“平移距离”为,求的最小值;
(3)若点的坐标为,记线段到的“平移距离”为,直接写出的取值范围.
相关知识点
推荐套卷
在平面直角坐标系中,的半径为1,,为外两点,.
给出如下定义:平移线段,得到的弦,分别为点,的对应点),线段长度的最小值称为线段到的“平移距离”.
(1)如图,平移线段得到的长度为1的弦和,则这两条弦的位置关系是 ;在点,,,中,连接点与点 的线段的长度等于线段到的“平移距离”;
(2)若点,都在直线上,记线段到的“平移距离”为,求的最小值;
(3)若点的坐标为,记线段到的“平移距离”为,直接写出的取值范围.
