如图, 中, , , ,点 从点 出发,沿边 以 的速度向终点 运动,过点 作 ,交边 (或 于点 .设点 的运动时间为 , 的面积为 .
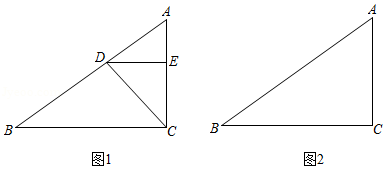
(1)当点 与点 重合时,求 的值;
(2)求 关于 的函数解析式,并直接写出自变量 的取值范围.
相关知识点
推荐套卷
如图, 中, , , ,点 从点 出发,沿边 以 的速度向终点 运动,过点 作 ,交边 (或 于点 .设点 的运动时间为 , 的面积为 .

(1)当点 与点 重合时,求 的值;
(2)求 关于 的函数解析式,并直接写出自变量 的取值范围.