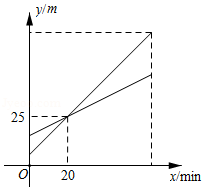
甲、乙两个探测气球分别从海拔 和 处同时出发,匀速上升 .如图是甲、乙两个探测气球所在位置的海拔 (单位: 与气球上升时间 (单位: 的函数图象.
(1)求这两个气球在上升过程中 关于 的函数解析式;
(2)当这两个气球的海拔高度相差 时,求上升的时间.
相关知识点
推荐套卷
甲、乙两个探测气球分别从海拔 和 处同时出发,匀速上升 .如图是甲、乙两个探测气球所在位置的海拔 (单位: 与气球上升时间 (单位: 的函数图象.
(1)求这两个气球在上升过程中 关于 的函数解析式;
(2)当这两个气球的海拔高度相差 时,求上升的时间.
