如图,三棱柱 中,侧棱垂直底面,
中,侧棱垂直底面, 是棱
是棱 的中点.
的中点.
(1)证明:平面 ⊥平面
⊥平面 ;
;
(2)平面 分此棱柱为两部分,求这两部分体积的比.
分此棱柱为两部分,求这两部分体积的比.
如图,平面 平面
平面 ,四边形
,四边形 是边长为2的正方形,
是边长为2的正方形, 为
为 上的点,且
上的点,且 平面
平面 .
.
(1)求证 平面
平面 ;
;
(2)设 ,是否存在
,是否存在 ,使二面角
,使二面角 的余弦值为
的余弦值为 ?若存在,求
?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
有三个命题:
①垂直于同一个平面的两条直线平行;
②∀x∈R,x4>x2;
③命题“所有能被2整除的整数都是偶数”的否定是:所有能被2整除的整数都不是偶数.
其中正确命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
如图,在三棱锥 中,
中, ,
, ,
, °,平面
°,平面 平面
平面 ,
, 、
、 分别为
分别为 、
、 中点.
中点.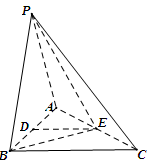
(1)求证: ;
;
(2)求二面角 的大小.
的大小.
如图所示,在四边形 中,
中, ,将四边形
,将四边形 沿对角线
沿对角线 折成四面体
折成四面体 ,使平面
,使平面 平面
平面 ,则下列结论正确的是 .
,则下列结论正确的是 .

(1) ;
;
(2) ;
;
(3) 与平面
与平面 所成的角为
所成的角为 ;
;
(4)四面体 的体积为
的体积为 .
.
一个正方体的展开图如图所示,A、B、C、D为原正方体的顶点,则在原来的正方体中( )

A.AB∥CD B.AB与CD相交
C.AB⊥CD D.AB与CD所成的角为60°
对于不重合的直线 和不重合的平面
和不重合的平面 ,下列命题错误的是( )
,下列命题错误的是( )
A.若 ,则 ,则 |
B.若 ,则 ,则 |
C.若 ,则 ,则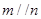 |
D.若 ,则 ,则 |
如图,在三棱柱 中,
中, ,
, ,
, ,
, 在底面ABC的射影为BC的中点,D为
在底面ABC的射影为BC的中点,D为 的中点.
的中点.
(1)证明: ;
;
(2)求直线 和平面
和平面 所成的角的正弦值.
所成的角的正弦值.