高中数学函数的基本性质试题

已知函数f（x）=（a，b，c∈Z）是奇函数，且f（1）=2，f（2）＜3．
（1）求a，b，c的值．
（2）判断函数f（x）在[1，+∞）上的单调性，并用定义证明你的结论．
（3）解关于t的不等式：f（﹣t²﹣1）+f（|t|+3）＞0．

已知函数f（x）是定义域在R上的奇函数，当x＞0时，f（x）=x²﹣2x．
（1）求出函数f（x）在R上的解析式；
（2）写出函数的单调区间．

已知函数f（x）=在区间（﹣2，+∞）上为增函数，则实数a的取值范围是 ．

设奇函数f（x）在[﹣1，1]上是增函数，且f（﹣1）=﹣1，若对所有的x∈[﹣1，1]及任意的a∈[﹣1，1]都满足f（x）≤t²﹣2at+1，则t的取值范围是（）

A．[﹣2，2]

B．{t|t≤﹣或t或=0}

C．[﹣，]

D．{t|t≤﹣2或t≥2或t=0}

定义在R上的偶函数f（x）满足：对任意的x₁，x₂∈（﹣∞，0]（x₁≠x₂），有，且f（2）=0，则不等式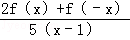＜0的解集是（）

A．（﹣∞，﹣2）∪（2，+∞）

B．（﹣∞，﹣2）∪（1，2）

C．（﹣2，1）∪（2，+∞）

D．（﹣2，1）∪（1，2）

已知函数f（x）=x³+x．
（1）判断函数f（x）的单调性与奇偶性，（不用证明结论）．
（2）若f（cosθ﹣m）+f（msinθ﹣2）＜0对θ∈R恒成立，求实数m的取值范围．

已知函数（x∈[1，+∞）且m＜1）．
（Ⅰ）用定义证明函数f（x）在[1，+∞）上为增函数；
（Ⅱ）设函数，若[2，5]是g（x）的一个单调区间，且在该区间上g（x）＞0恒成立，求实数m的取值范围．

已知函数f（x）在其定义域（﹣∞，0）上是减函数，且f（1﹣m）＜f（m﹣3），则实数m的取值范围是（）

A．（﹣∞，2）

B．（0，1）

C．（0，2）

D．（1，2）

下列函数中，定义域是R且为增函数的是（）

A．y=e^﹣x

B．y=x^3

C．y=lnx

D．y=|x|

函数的极小值点______________．

函数，则（）

A．仅有最小值

B．仅有最大值

C．既有最小值0，也有最大值

D．既无最大值，也无最小值

函数在区间上是减函数，则实数的取值范围是（）

A．

B．

C．

D．

函数的极小值点______________．

函数，则（）

A．仅有最小值

B．仅有最大值

C．既有最小值0，也有最大值

D．既无最大值，也无最小值

已知函数是定义在上的增函数，函数的图象关于点对称，若对
任意的，不等式恒成立，则的取值范围是 ．