已知函数f(x)=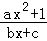 (a,b,c∈Z)是奇函数,且f(1)=2,f(2)<3.
(a,b,c∈Z)是奇函数,且f(1)=2,f(2)<3.
(1)求a,b,c的值.
(2)判断函数f(x)在[1,+∞)上的单调性,并用定义证明你的结论.
(3)解关于t的不等式:f(﹣t2﹣1)+f(|t|+3)>0.
相关知识点
推荐套卷
已知函数f(x)=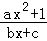 (a,b,c∈Z)是奇函数,且f(1)=2,f(2)<3.
(a,b,c∈Z)是奇函数,且f(1)=2,f(2)<3.
(1)求a,b,c的值.
(2)判断函数f(x)在[1,+∞)上的单调性,并用定义证明你的结论.
(3)解关于t的不等式:f(﹣t2﹣1)+f(|t|+3)>0.