如图,在矩形中,,,点是边的中点,反比例函数的图象经过点,交边于点,直线的解析式为.
(1)求反比例函数的解析式和直线的解析式;
(2)在轴上找一点,使的周长最小,求出此时点的坐标;
(3)在(2)的条件下,的周长最小值是 .
推荐套卷
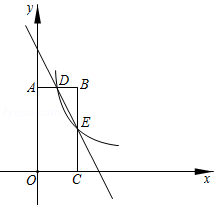
如图,在矩形中,,,点是边的中点,反比例函数的图象经过点,交边于点,直线的解析式为.
(1)求反比例函数的解析式和直线的解析式;
(2)在轴上找一点,使的周长最小,求出此时点的坐标;
(3)在(2)的条件下,的周长最小值是 .
