一个玩具盘由一个直径为 米的半圆
米的半圆 和一个矩形
和一个矩形 构成,
构成,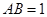 米,如图所示.小球从
米,如图所示.小球从 点出发以
点出发以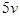 的速度沿半圆
的速度沿半圆 轨道滚到某点
轨道滚到某点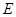 处后,经弹射器以
处后,经弹射器以 的速度沿与点
的速度沿与点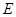 切线垂直的方向弹射到落袋区
切线垂直的方向弹射到落袋区 内,落点记为
内,落点记为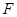 .设
.设 弧度,小球从
弧度,小球从 到
到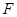 所需时间为
所需时间为 .
.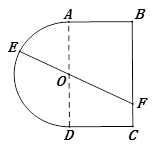
(1)试将 表示为
表示为 的函数
的函数 ,并写出定义域;
,并写出定义域;
(2)求时间 最短时
最短时 的值.
的值.
推荐套卷
一个玩具盘由一个直径为 米的半圆
米的半圆 和一个矩形
和一个矩形 构成,
构成,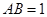 米,如图所示.小球从
米,如图所示.小球从 点出发以
点出发以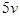 的速度沿半圆
的速度沿半圆 轨道滚到某点
轨道滚到某点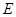 处后,经弹射器以
处后,经弹射器以 的速度沿与点
的速度沿与点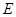 切线垂直的方向弹射到落袋区
切线垂直的方向弹射到落袋区 内,落点记为
内,落点记为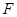 .设
.设 弧度,小球从
弧度,小球从 到
到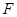 所需时间为
所需时间为 .
.
(1)试将 表示为
表示为 的函数
的函数 ,并写出定义域;
,并写出定义域;
(2)求时间 最短时
最短时 的值.
的值.