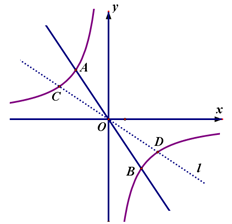
(本题共12分)如图,在平面直角坐标系中,正比例函数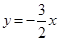 与反比例函数
与反比例函数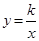 的图象交于A、B两点,且点A的横坐标为
的图象交于A、B两点,且点A的横坐标为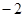 .
.
(1)求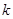 值;
值;
(2)利用图象,直接写出不等式
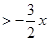 的解集;
的解集;
(3)过坐标原点O的另一条直线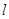 交反比例函数
交反比例函数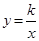 的图象于C、D两点,且C点的纵坐标为2.依次连接AC、CB、BD、DA,求以A、C、B、D为顶点组成的四边形的面积S.
的图象于C、D两点,且C点的纵坐标为2.依次连接AC、CB、BD、DA,求以A、C、B、D为顶点组成的四边形的面积S.
推荐套卷
(本题共12分)如图,在平面直角坐标系中,正比例函数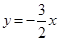 与反比例函数
与反比例函数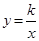 的图象交于A、B两点,且点A的横坐标为
的图象交于A、B两点,且点A的横坐标为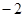 .
.
(1)求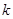 值;
值;
(2)利用图象,直接写出不等式
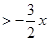 的解集;
的解集;
(3)过坐标原点O的另一条直线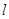 交反比例函数
交反比例函数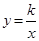 的图象于C、D两点,且C点的纵坐标为2.依次连接AC、CB、BD、DA,求以A、C、B、D为顶点组成的四边形的面积S.
的图象于C、D两点,且C点的纵坐标为2.依次连接AC、CB、BD、DA,求以A、C、B、D为顶点组成的四边形的面积S.