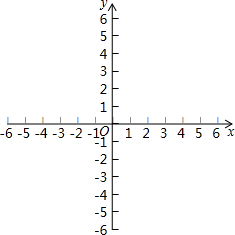已知直线 与 轴交于点 ,与 轴交于点 ,且与双曲线 交于点 .
(1)试确定双曲线的函数表达式;
(2)将 沿 轴翻折后,得到 ,画出 的图象,并求出 的函数表达式;
(3)在(2)的条件下,点 是线段 上点(不包括端点),过点 作 轴的平行线,分别交 于点 ,交双曲线于点 ,求 的取值范围.
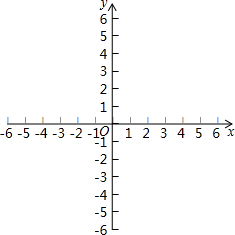
推荐套卷
已知直线 与 轴交于点 ,与 轴交于点 ,且与双曲线 交于点 .
(1)试确定双曲线的函数表达式;
(2)将 沿 轴翻折后,得到 ,画出 的图象,并求出 的函数表达式;
(3)在(2)的条件下,点 是线段 上点(不包括端点),过点 作 轴的平行线,分别交 于点 ,交双曲线于点 ,求 的取值范围.