某医药研究所开发了一种新药,在试验时发现,如果成人按规定剂量服用2小时时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随服药后时间x(小时)的变化如图所示,当成人按规定剂量服药后。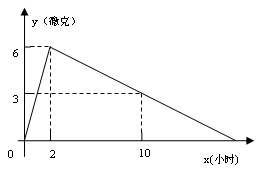
⑴分别求出x<2与x>2时y与x的函数关系式
⑵如果每毫升血液中含药量为或3微克以上时,在治疗时是有效的,那么这个有效时间是多长?
相关知识点
推荐套卷
某医药研究所开发了一种新药,在试验时发现,如果成人按规定剂量服用2小时时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随服药后时间x(小时)的变化如图所示,当成人按规定剂量服药后。
⑴分别求出x<2与x>2时y与x的函数关系式
⑵如果每毫升血液中含药量为或3微克以上时,在治疗时是有效的,那么这个有效时间是多长?