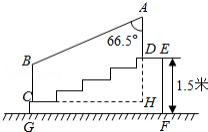
如图，某城市市民广场一入口处有五级高度相等的小台阶．已知台阶_优题课试题网

首页 / 初中数学 / 试题详细

更新 2022-09-04
科目数学
题型解答题
难度中等
浏览 138

如图，某城市市民广场一入口处有五级高度相等的小台阶．已知台阶总高1.5米，为了安全，现要做一个不锈钢扶手 $AB$ 及两根与 $FG$ 垂直且长为1米的不锈钢架杆 $AD$ 和 $BC$ （杆子的底端分别为 $D$ 、 $C)$ ，且 $∠ DAB = 66.5 °$ ．（参考数据： $\cos 66.5 ° \approx 0.40$ ， $\sin 66.5 ° \approx 0.92)$

（1）求点 $D$ 与点 $C$ 的高度差 $DH$ ；

（2）求所有不锈钢材料的总长度（即 $AD + AB + BC$ 的长，结果精确到0.1米）

登录免费查看答案和解析

相关试题

如图， $ΔABC$ 中， $AB = AC$ ，以 $AC$ 为直径的 $⊙ O$ 交 $BC$ 于点 $D$ ，点 $E$ 为 $AC$ 延长线上一点，且 $∠ CDE = \frac{1}{2} ∠ BAC$ ．

（1）求证： $DE$ 是 $⊙ O$ 的切线；

（2）若 $AB = 3 BD$ ， $CE = 2$ ，求 $⊙ O$ 的半径．

题型：未知
难度：未知

收藏答案/解析

已知关于 $x$ 的一元二次方程 $x^{2} - 6 x + 2 a + 5 = 0$ 有两个不相等的实数根 $x_{1}$ ， $x_{2}$ ．

（1）求 $a$ 的取值范围；

（2）若 $x_{1}^{2} + x_{2}^{2} - x_{1} x_{2} ⩽ 30$ ，且 $a$ 为整数，求 $a$ 的值．

题型：未知
难度：未知

收藏答案/解析

第一盒中有2个白球、1个黄球，第二盒中有1个白球、1个黄球，这些球除颜色外无其他差别．

（1）若从第一盒中随机取出1个球，则取出的球是白球的概率是　　．

（2）若分别从每个盒中随机取出1个球，请用列表或画树状图的方法求取出的两个球中恰好1个白球、1个黄球的概率．

题型：未知
难度：未知

收藏答案/解析

如图，拦水坝的横断面为梯形 $ABCD$ ， $AD = 3 m$ ，坝高 $AE = DF = 6 m$ ，坡角 $α = 45 °$ ， $β = 30 °$ ，求 $BC$ 的长．

题型：未知
难度：未知

收藏答案/解析

先化简，再求值： $(1 - \frac{1}{a}) \div (\frac{a^{2} + 1}{a} - 2)$ ，其中 $a = \sqrt{3} + 1$ ．

题型：未知
难度：未知

收藏答案/解析

相关知识点

解直角三角形的应用

推荐套卷

热门套卷

粤ICP备20024846号

粤公网安备

粤公网安备 44130202000953号

Copyright ©2020-2025 优题课 youtike.com 版权所有 Powered by：Youtike Platform 6.8.8

声明：本网站部分内容由互联网用户自发贡献自行上传，本网站不拥有所有权，也不承担相关法律责任。
如果您发现有涉嫌版权的内容，欢迎发送邮件至：service@youtike.com 或联系QQ：267757 进行举报，一经查实，本站将立刻删除涉嫌侵权内容。