已知两直线L1:y=k1x+b1,L2:y=k2x+b2,若L1⊥L2,则有k1•k2=﹣1.
(1)应用:已知y=2x+1与y=kx﹣1垂直,求k;
(2)直线经过A(2,3),且与y=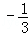 x+3垂直,求解析式.
x+3垂直,求解析式.
相关知识点
推荐套卷
已知两直线L1:y=k1x+b1,L2:y=k2x+b2,若L1⊥L2,则有k1•k2=﹣1.
(1)应用:已知y=2x+1与y=kx﹣1垂直,求k;
(2)直线经过A(2,3),且与y=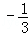 x+3垂直,求解析式.
x+3垂直,求解析式.