在平面直角坐标系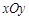 中,已知圆
中,已知圆 :
: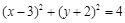 ,圆
,圆 :
:
 (
( ,且
,且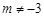 ).
).
(1)设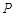 为坐标轴上的点,满足:过点P分别作圆
为坐标轴上的点,满足:过点P分别作圆 与圆
与圆 的一条切线,切点分别为
的一条切线,切点分别为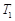 、
、 ,使得
,使得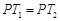 ,试求出所有满足条件的点
,试求出所有满足条件的点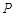 的坐标;
的坐标;
(2)若斜率为正数的直线 平分圆
平分圆 ,求证:直线
,求证:直线 与圆
与圆 总相交.
总相交.
相关知识点
推荐套卷
在平面直角坐标系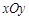 中,已知圆
中,已知圆 :
: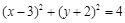 ,圆
,圆 :
:
 (
( ,且
,且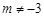 ).
).
(1)设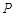 为坐标轴上的点,满足:过点P分别作圆
为坐标轴上的点,满足:过点P分别作圆 与圆
与圆 的一条切线,切点分别为
的一条切线,切点分别为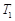 、
、 ,使得
,使得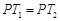 ,试求出所有满足条件的点
,试求出所有满足条件的点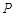 的坐标;
的坐标;
(2)若斜率为正数的直线 平分圆
平分圆 ,求证:直线
,求证:直线 与圆
与圆 总相交.
总相交.