在平面直角坐标系xoy中,已知曲线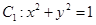 ,将
,将 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的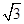 、2倍后得到曲线
、2倍后得到曲线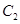 ,以平面直角坐标系xoy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
,以平面直角坐标系xoy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线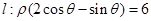
(1) 试写出直线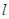 的直角坐标方程;
的直角坐标方程;
(2) 在曲线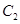 上求一点P,使点P到直线
上求一点P,使点P到直线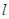 的距离最大,并求出此最大值。
的距离最大,并求出此最大值。
相关知识点
推荐套卷
在平面直角坐标系xoy中,已知曲线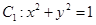 ,将
,将 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的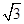 、2倍后得到曲线
、2倍后得到曲线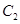 ,以平面直角坐标系xoy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
,以平面直角坐标系xoy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线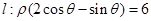
(1) 试写出直线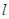 的直角坐标方程;
的直角坐标方程;
(2) 在曲线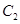 上求一点P,使点P到直线
上求一点P,使点P到直线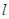 的距离最大,并求出此最大值。
的距离最大,并求出此最大值。