(本小题满分12分)某中学生物兴趣小组在学校生物园地种植了一批名贵树苗,为了解树苗的生长情况,从这批树苗中随机地测量了其中50棵树苗的高度(单位:厘米),并把这些高度列成了如下的频数分布表:
(1)在这批树苗中,其高度在85厘米以上的树苗大约有多少棵?
(2)这批树苗的平均高度大约是多少?;
(3)为了进一步获得研究资料,若从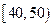 组中移出一棵树苗,从
组中移出一棵树苗,从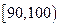 组中移出两棵树苗进行试验研究,则
组中移出两棵树苗进行试验研究,则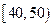 组中的树苗A和
组中的树苗A和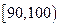 组中的树苗C同时被移出的概率是多少?
组中的树苗C同时被移出的概率是多少?
推荐套卷
(本小题满分12分)某中学生物兴趣小组在学校生物园地种植了一批名贵树苗,为了解树苗的生长情况,从这批树苗中随机地测量了其中50棵树苗的高度(单位:厘米),并把这些高度列成了如下的频数分布表:
(1)在这批树苗中,其高度在85厘米以上的树苗大约有多少棵?
(2)这批树苗的平均高度大约是多少?;
(3)为了进一步获得研究资料,若从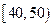 组中移出一棵树苗,从
组中移出一棵树苗,从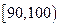 组中移出两棵树苗进行试验研究,则
组中移出两棵树苗进行试验研究,则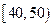 组中的树苗A和
组中的树苗A和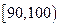 组中的树苗C同时被移出的概率是多少?
组中的树苗C同时被移出的概率是多少?