如图,在△ABD和△ACE中,有下列四个等式:①AB="AC" ②AD="AE" ③∠1=∠2 ④BD=CE.请你以其中三个等式作为题设,余下的作为结论,写出一个真命题(要求写出已知,求证及证明过程)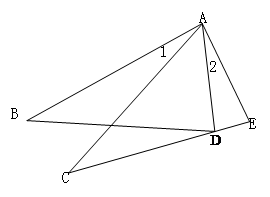
相关知识点
推荐套卷
如图,在△ABD和△ACE中,有下列四个等式:①AB="AC" ②AD="AE" ③∠1=∠2 ④BD=CE.请你以其中三个等式作为题设,余下的作为结论,写出一个真命题(要求写出已知,求证及证明过程)