如图，甲、乙两人分别从A(1，
)、B(6，0)两点同时出发，点O为坐标原点，甲沿AO方向、乙沿BO方向均以4km/h的速度行驶，th后，甲到达M点，乙到达N点．
(1)请说明甲、乙两人到达O点前，MN与AB不可能平行．
(2)当t为何值时，△OMN∽△OBA？
(3)甲、乙两人之间的距离为MN的长，设s＝MN2，求s与t之间的函数关系式，并求甲、乙两人之间距离的最小值．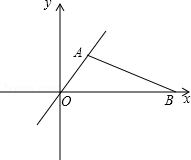
推荐套卷
如图，甲、乙两人分别从A(1，)、B(6，0)两点同时出发，点O为坐标原点，甲沿AO方向、乙沿BO方向均以4km/h的速度行驶，th后，甲到达M点，乙到达N点．
(1)请说明甲、乙两人到达O点前，MN与AB不可能平行．
(2)当t为何值时，△OMN∽△OBA？
(3)甲、乙两人之间的距离为MN的长，设s＝MN2，求s与t之间的函数关系式，并求甲、乙两人之间距离的最小值．
粤公网安备 44130202000953号