我们在配平化学方程式时,对于某些简单的方程式可以用观察法配平,对于某些复杂的方程式,还可以尝试运用方程的思想和比例的方法.例如方程式: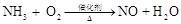 ,可以设NH3的系数为1,其余三项系数分别为x、y、z,即:
,可以设NH3的系数为1,其余三项系数分别为x、y、z,即: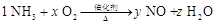 ,依据反应前后各元素守恒,得:
,依据反应前后各元素守恒,得: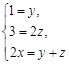 ,解之得四项系数之比为1:
,解之得四项系数之比为1: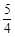 :1:
:1: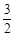 ,扩大4倍得整数比为4:5:4:6,即配平结果为:
,扩大4倍得整数比为4:5:4:6,即配平结果为: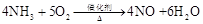 .请运用上述方法,配平化学方程式:
.请运用上述方法,配平化学方程式: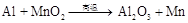 .
.
相关知识点
推荐套卷
我们在配平化学方程式时,对于某些简单的方程式可以用观察法配平,对于某些复杂的方程式,还可以尝试运用方程的思想和比例的方法.例如方程式: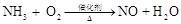 ,可以设NH3的系数为1,其余三项系数分别为x、y、z,即:
,可以设NH3的系数为1,其余三项系数分别为x、y、z,即: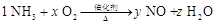 ,依据反应前后各元素守恒,得:
,依据反应前后各元素守恒,得: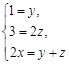 ,解之得四项系数之比为1:
,解之得四项系数之比为1: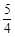 :1:
:1: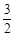 ,扩大4倍得整数比为4:5:4:6,即配平结果为:
,扩大4倍得整数比为4:5:4:6,即配平结果为: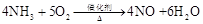 .请运用上述方法,配平化学方程式:
.请运用上述方法,配平化学方程式: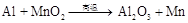 .
.