锐角△ABC中，BC=6，S△ABC=12，两动点M，N分别在边AB，AC上滑动，且MN∥BC，以MN为边向下作正方形MPQN，设其边长为x，正方形MPQN与△ABC公共部分的面积为y，(y>0)．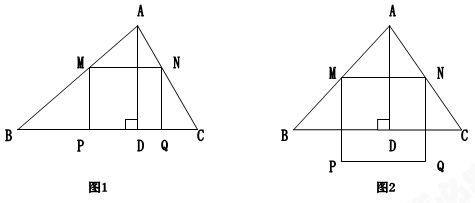
(1)△ABC中边BC上高AD= _______；
(2)当x= _______时PQ恰好落在边BC上(如图1)；
(3)当PQ在△ABC外部时(如图2)，求y关于x的函数关系式，并求出z为何值时y
最大，最大值是多少?1
相关试题
，∴
；
，∴
；……………………………
。如图，铁路上A，B两点相距25千米，DA⊥AB于A，CB⊥AB于B，已知DA长15千米，CB长为10千米，现在要在铁路AB上建一个农产品收购站E，使得C、D两村到E站的距离相等，则E站应建在离A站多少千米处？
的平方根是
的立方根是3，求
的平方根。
在数轴上的位置如图所示，试化简
。(5分)
相关知识点
推荐套卷
粤公网安备 44130202000953号